本文針對傳統多尺度熵在多尺度化過程中信息丟失問題，提出一種加權多重多尺度熵特征提取算法。該算法在各尺度上構建了從大到小的多重數據序列，考慮多重數據序列對該尺度樣本熵的貢獻程度不同，計算各個序列在該尺度序列中所占比重，以此作為系數重構各尺度樣本熵。相比于傳統多尺度熵算法，該算法不但克服了信息丟失問題，還充分考慮了序列的相關性與對總熵值的貢獻程度，減小了尺度間的波動，更能挖掘腦電信號的細節信息。基于該算法，本文分析了孤獨癥（ASD）兒童腦電信號特征，與樣本熵、傳統多尺度熵及延擱取值法多重多尺度熵算法比較，分類準確率分別提高了 23.0%、10.4% 與 6.4%。基于該算法對比分析孤獨癥兒童與對照組健康兒童的 19 通道腦電信號，結果表明除 FP2 通道外，其余通道的熵值均顯示健康兒童略高于孤獨癥兒童，且 F3、F7、F8、C3、P3 通道的熵值差異具有統計學意義（P<0.05）。本文通過對各個腦區加權多重多尺度熵進行分類，發現前顳葉區域通道（F7、F8）的分類準確率最高，表明前顳葉可以作為評估孤獨癥兒童腦功能狀態的敏感腦區。
引用本文： 李昕, 安占周, 李秋月, 史春燕, 張潔, 康健楠. 加權多重多尺度熵及其在孤獨癥兒童腦電信號分析中的應用. 生物醫學工程學雜志, 2019, 36(1): 33-39, 49. doi: 10.7507/1001-5515.201806047 復制
引言
孤獨癥，也稱自閉癥，是一種起源于兒童早期，以社會交往和溝通障礙、興趣范圍狹窄及重復刻板行為為主要特征的廣泛性發育障礙[1-2]。據 2015 年調查數據顯示，孤獨癥發病率已經達到了 1∶45[3]。
國內對孤獨癥研究從最初的心理學和行為學研究，逐漸向腦功能電生理分析和影像學研究方向發展。腦電信號通過記錄大腦皮層的電生理活動，能夠表現出大腦的神經系統內部活動[4]。Duffy 等[5]通過大量的研究，發現了一種穩定的腦電譜耦合模式，可以有效地識別孤獨癥兒童。Dawson 等[6]比較了孤獨癥兒童和對照組兒童的腦電信號功率譜，該項研究結果表明，相對于對照組兒童，孤獨癥兒童在前額和顳區的腦電信號功率譜偏低，左半球比右半球更加明顯。Pineda 等[7]通過神經反饋訓練發現，經過訓練的孤獨癥患者 mu 頻帶（10～13 Hz）功率和相干性降低。由此可見，腦電信號分析是研究孤獨癥兒童腦功能狀態的一種有效方法。
腦電信號具有非線性和非平穩性的特點[8]。常用的腦電信號非線性分析方法主要有：經驗模態分解（empirical mode decomposition，EMD）算法和赫斯特（Hurst）指數分析等[9]。熵算法能夠刻畫系統所處狀態的無序性和混亂程度，有助于更深入地理解腦電信號中的動態變化以及大腦中潛在的混沌狀態，且與其他非線性方法相比，熵具有對數據長度依賴更小的優點[10]。Srinivasan 等[11]采用近似熵（approximate entropy，ApEn）提取腦電信號中的特征，基于概率神經網絡（probabilistic neural network，PNN）對腦電數據進行分類，得到了 84.5% 的準確率。Catarino 等[12]基于多尺度熵（multiscale entropy，MSE）的方法提取孤獨癥兒童腦電信號特征，結果表明孤獨癥患者的腦電復雜度（complexity，CPX）明顯降低。
多尺度熵特征提取算法能夠充分挖掘腦電信號隱藏的細節信息。Bornas 等[13]和 Thuraisingham 等[14]證明了在反映腦電信號特征方面，多尺度熵算法能夠提取到更多的細節信息。Li 等[15]將多尺度熵算法與排序熵（permutation entropy，PE）結合，克服了排序熵的不足，更好地描述了腦電信號特性，同時證明多尺度排序熵在腦電信號分析中更有優勢。
本文針對傳統多尺度熵在多尺度化過程中，因序列縮短而造成的信息丟失問題，提出一種加權多重多尺度熵特征提取方法。該算法基于經驗模態分解多尺度分解思想，考慮到對每個數據的充分利用，且不改變原始序列的波動形式，加權多重多尺度熵在每個尺度上以尺度為時間窗參數，構建等長的時間窗，依次從每個時間窗提取從大到小的數據點，構建多重數據序列。將該尺度均值粗粒化（coarse graining，CG）后的序列作為基點，計算該序列與多重序列的相關系數，進一步計算每重序列相關系數占該尺度多重序列總相關系數的比重，作為相關權重，再運用加權理論計算每個尺度的總樣本熵。相比于傳統多尺度熵在每個尺度構建一個序列，以及單一多重多尺度熵認為多重序列貢獻率相同的簡單處理方法，基于加權多重多尺度熵特征提取算法不但克服了信息丟失問題，還充分考慮了多重序列間的相關性與對總熵值的貢獻程度，減小了尺度間的波動，更能挖掘腦電信號的細節信息。
基于加權多重多尺度熵算法，本文對孤獨癥兒童和健康對照組兒童靜息態腦電信號進行特征提取，通過分析孤獨癥兒童和健康兒童 19 通道的加權多重多尺度熵，結合統計產品與服務解決方案（statistical product and service solutions，SPSS）軟件數據分析和支持向量機（support vector machine，SVM）的分類，探究孤獨癥兒童與健康兒童腦電數據復雜性的差異，由此探究孤獨癥兒童的異常通道，定位其敏感腦區，為孤獨癥兒童的腦功能狀態評估與分析提供一種有效的新方法。
1 加權多重多尺度樣本熵
1.1 樣本熵
樣本熵（sample entropy，SampEn）（以符號 SampEn 表示）是一種衡量時間序列復雜度的方法，是對近似熵算法的改進[16]。對于給定的時間序列{x1，x2，
，xi，
，xN}，構建一個 m 維的矢量，如式（1）所示：
 |
定義 d ［xi，xj］為兩個矢量元素 xi 和 xj 之間的最大距離，如式（2）所示：
 |
然后，定義閾值 r，統計 d［xi，xj］小于閾值 r 的數目 n，計算 n 與 d［xi，xj］數目的比值，記為 Cim（r），如式（3）所示：
 |
N ? m 是 d［xi，xj］的總元素數量。如式（4）所示，可得到所有 Cim（r）的平均值 Cm（r）：
 |
在此基礎上，將維數加 1，使之變為 m+1 維的矢量，重復上述步驟得到 Cm+1（r）。然后，計算該尺度樣本熵值，如式（5）所示：
 |
其中，m 是嵌入維數，r 是閾值。
1.2 加權多重多尺度樣本熵
加權多重多尺度熵算法針對傳統多尺度熵隨著尺度增大而使數據序列縮短所造成的信息丟失問題，基于經驗模態分解中多尺度分解思想，在每個尺度構建多重序列，考慮每重序列的相關貢獻程度，運用加權理論，計算每個尺度的總樣本熵，最大程度地克服了信息丟失問題。加權多重多尺度熵算法的具體步驟如下：
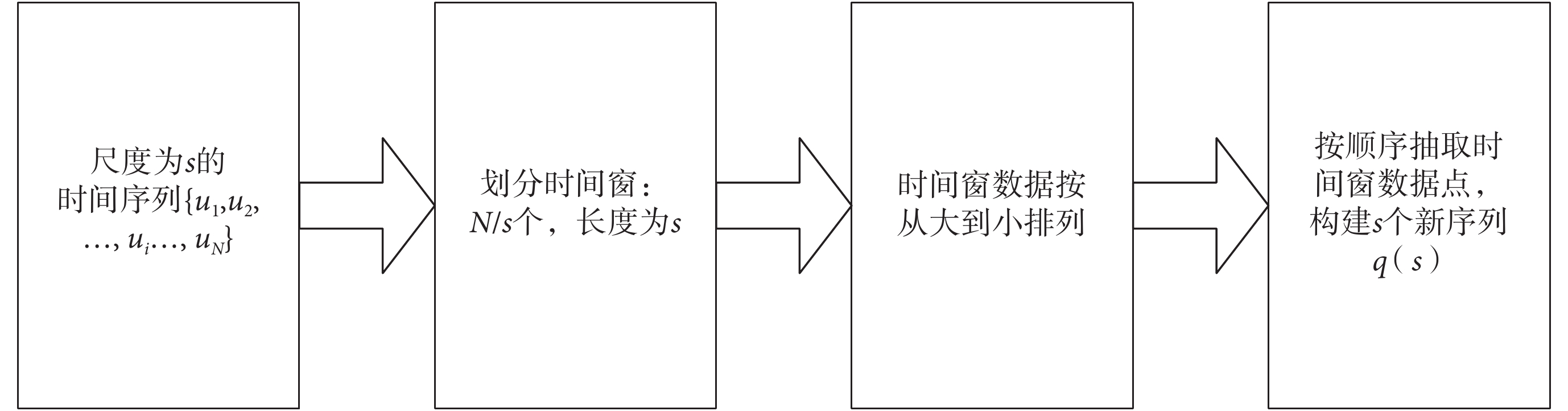
（1）對于給定的時間序列{u1，u2，
，ui，
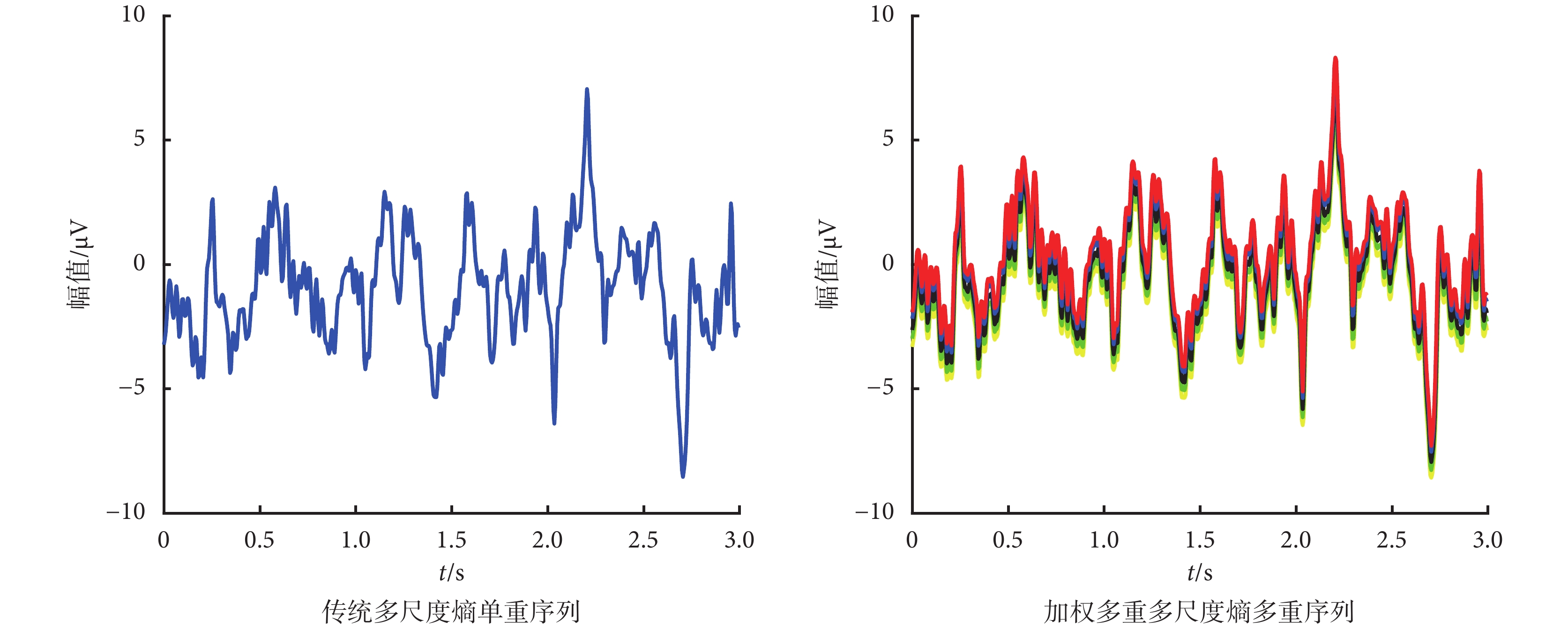
，uN}，構建各尺度多重序列，步驟如圖 1 所示。每個尺度構建 s 個新序列。即當 s = 1 時，新序列只有一個，而 s
1 時，該尺度下的新序列有 s 個。如圖 2 所示為尺度為 5 時傳統多尺度熵單重序列與加權多重多尺度熵多重序列的對比。由圖 2 可知，在尺度為 5 時，傳統多尺度熵只構建了單重數據序列，而加權多重多尺度熵則構建了與尺度相等的五重數據序列，每重序列的波動形式與傳統多尺度熵的單重序列一致，且五重序列按幅值從大到小排列。加權多重多尺度熵構建多重序列，通過增加重構的序列數量，可以避免傳統多尺度熵的信息丟失問題。
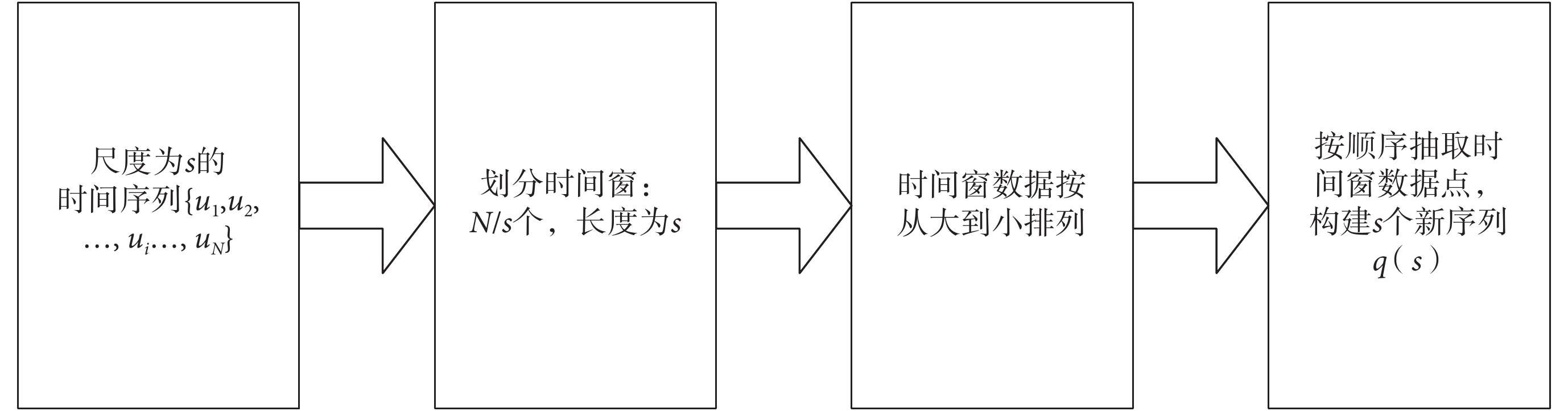圖1
多重序列構建
Figure1.
Multiple sequence construction
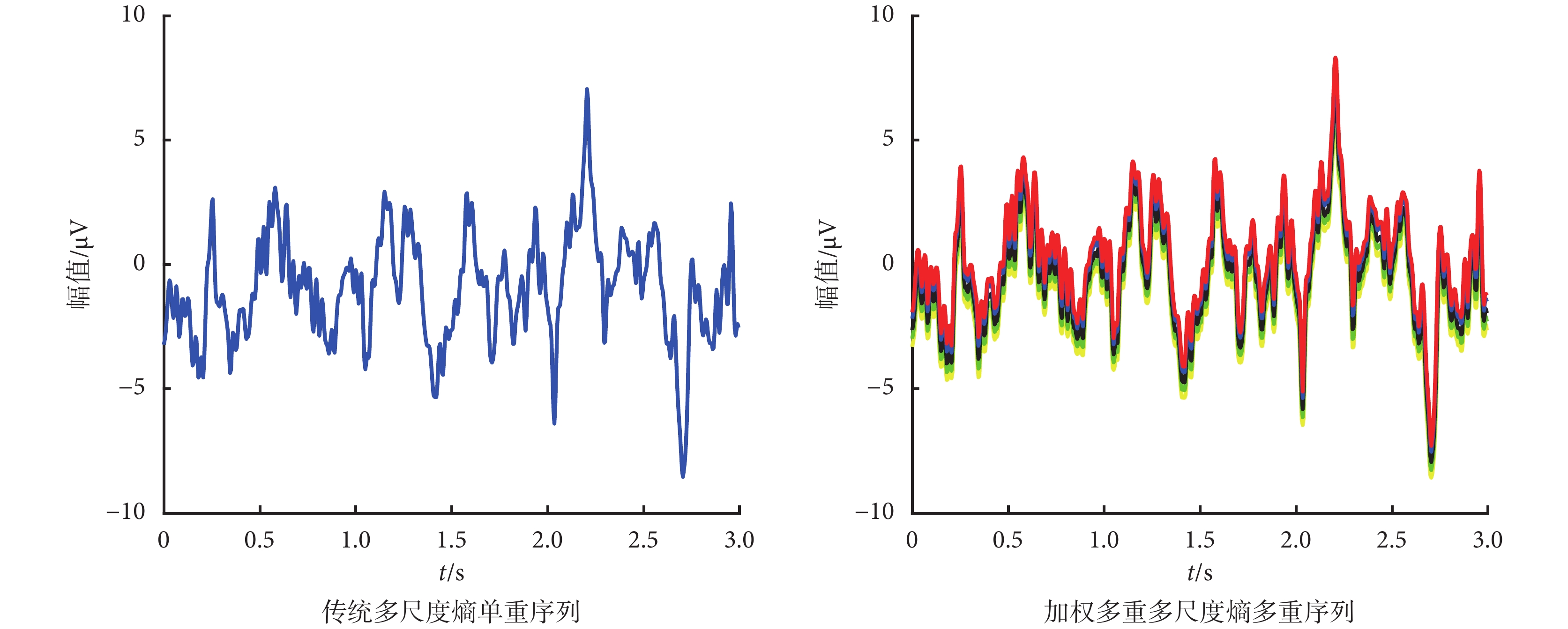圖2
尺度為 5 時序列對比
Figure2.
Comparison of sequences with scale of 5
（2）然后，計算每重序列在該尺度下的比重：對于給定的時間序列{u1，u2，
，ui，
，uN}，進行均值粗粒化處理，得到每個尺度下的新序列 Q（s）。以新序列 Q（s） 為基點，計算步驟（1）中的每個尺度下多重序列的相關系數[17]，如式（6）所示：
 |
（3）進一步計算每個序列在該尺度下所占的權重 w，如式（7）所示：
 |
（4）再進一步計算多重序列的樣本熵，如式（8）所示：
 |
（5）最后計算該尺度下的樣本熵（以符號 qSampEn 表示），如式（9）所示：
 |
2 腦電數據采集及預處理
2.1 腦電數據采集
本試驗采用 128 導聯腦電圖分析系統（Net Station4.5.2，Electrical Geodesics Inc，美國）進行時長 5 min 的靜息態腦電信號采集。按照國際標準的 10/20 系統將 Cz 電極作為參考，同時設置每個電極小于 50 kΩ 的阻抗值，參考電極和雙側乳突處的電極阻抗值則小于 10 kΩ，采樣率為 1 000 Hz。
本文共招募了 50 名兒童受試者，其中 25 名孤獨癥兒童（試驗組）與 25 名健康兒童（對照組）。試驗組兒童，年齡范圍在 4～8 歲，平均年齡為（6.30±1.43）歲；對照組兒童，年齡范圍在 4～8 歲，平均年齡為（6.43±1.27）歲。試驗前，要求受試者靜息 2 min，以便受試者進入放松狀態。試驗過程在安靜的房間中進行，期間保持安靜狀態，盡可能避免或減小外界干擾。本試驗所有受試人員及其家長均簽署了知情同意書。
2.2 腦電數據預處理
數據預處理步驟如下：
（1）壞通道替換，將有問題通道的數據由周圍通道數據均值進行替換。
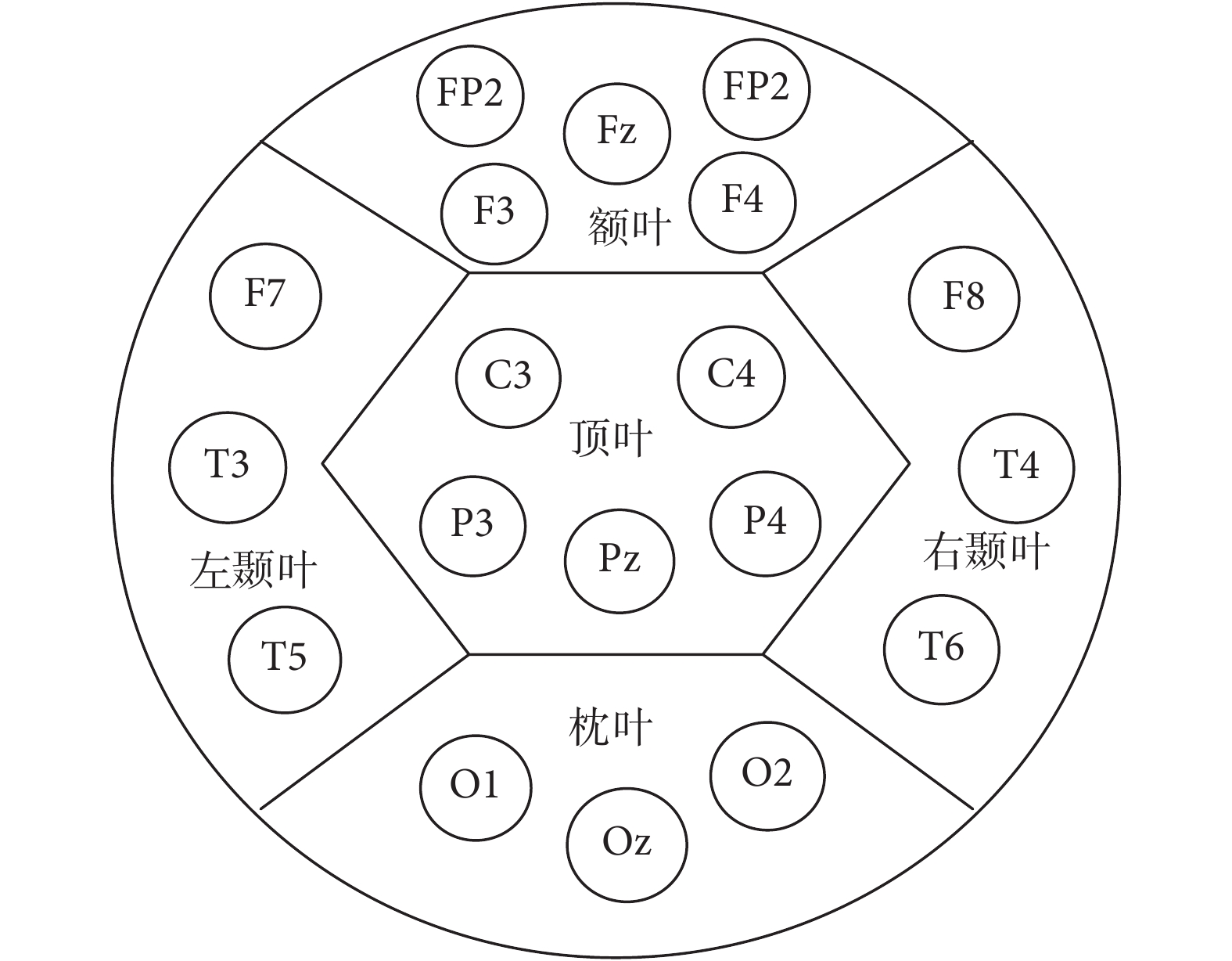
（2）從 128 個通道中按照國際標準的 10/20 系統選出 19 個通道，分別位于額葉、頂葉、枕葉、左顳葉和右顳葉等 5 個腦區，如圖 3 所示。
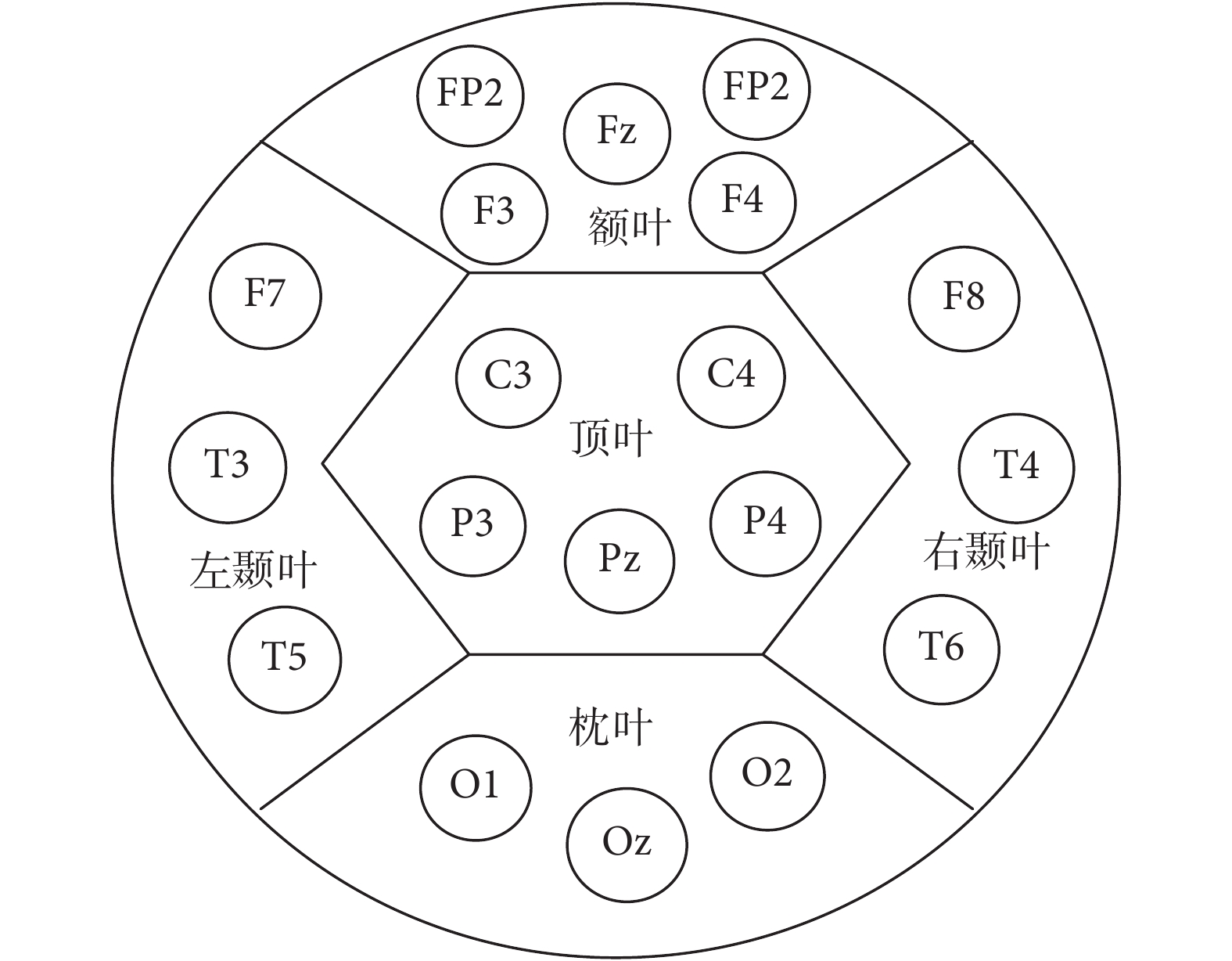圖3
19 通道腦區分布圖
Figure3.
Brain distribution map of 19 channels
（3）去除眨眼、眼動、呼吸偽跡、工頻干擾、肌電、心電、突變斜坡和離群值等偽跡信號，進行 0.5～45.0 Hz 的帶通濾波。
3 腦電數據處理結果與分析
3.1 多尺度參數設置
根據以往的研究，嵌入維數 m 設置為 2，閾值設置為 r = 0.15 × std（x），其中 std（x）為時間序列 x 的標準差。最大尺度 s 設置為 15，這樣就不會由于尺度過小而使特征體現不出明顯的趨勢，也不會因為尺度過大而造成計算復雜的問題。
3.2 多尺度熵對比分析
對比分析 25 名孤獨癥兒童與 25 名健康兒童腦電信號特征參數，分別提取傳統多尺度樣本熵、延擱取值法多重多尺度樣本熵與加權多重多尺度樣本熵特征量。所謂延擱取值法多重多尺度熵是對傳統多尺度熵算法的一種改進，即在移動均值粗粒化（moving averaging，MA）的基礎上，運用延擱取值法在每個尺度上構建多重數列，即由第一個數據點開始，相隔相關尺度個數據點依次取值，從而構建多重數列，再求取多重數列的樣本熵均值作為該尺度的樣本熵值。延擱取值法多重多尺度熵具體算法步驟如下：
（1）對給定的時間序列{x1，x2，
，xi，
，xN}，以尺度為 s 進行移動均值粗粒化，得到新序列 Z（s），長度為 N ? s + 1。再對新序列 Z（s）以尺度為 s 為參數進行延擱法取值，構建多重序列 V（s），長度為 l。如式（10）、（11）所示：
 |
 |
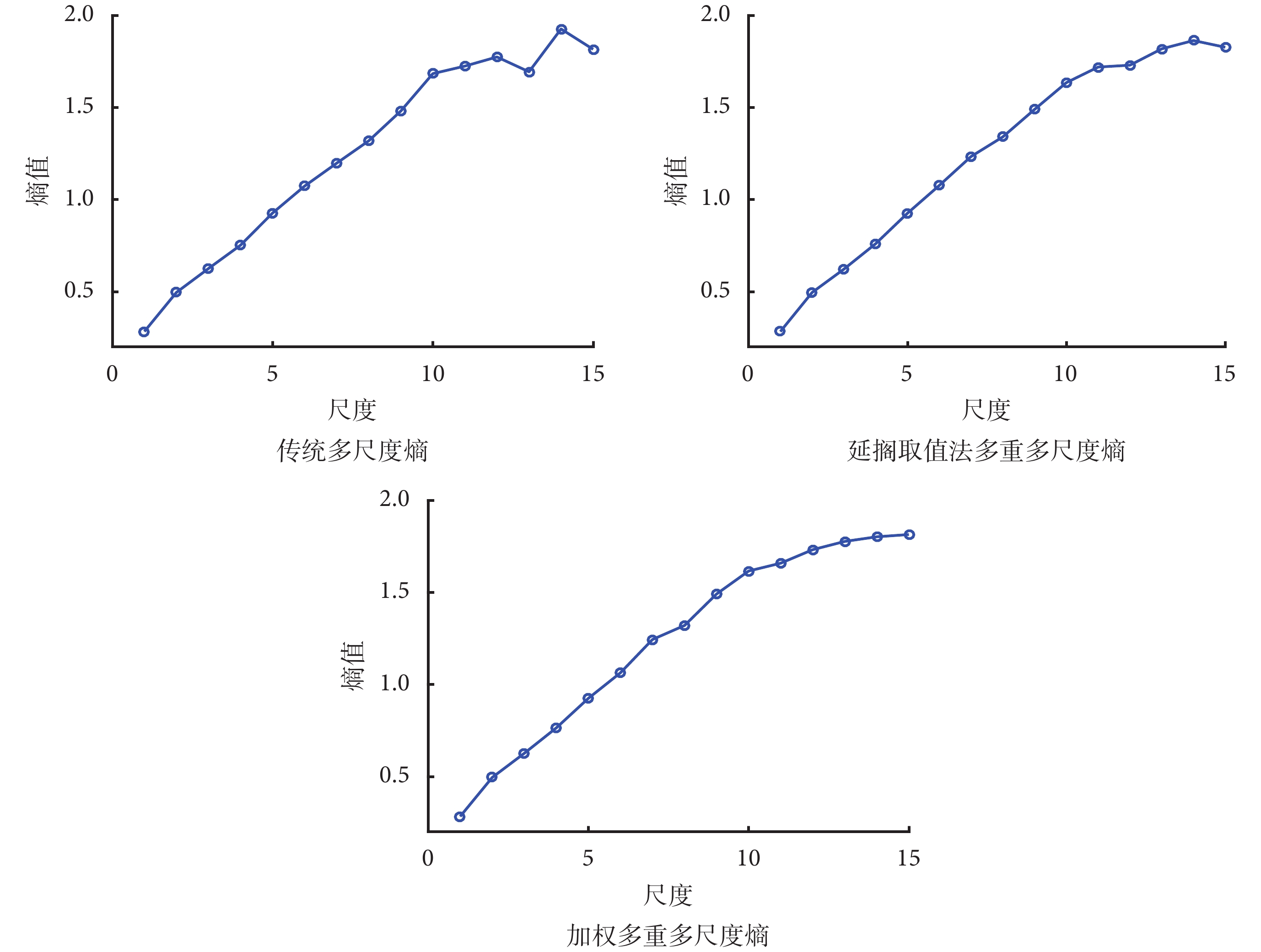
最后計算每個尺度構建的多重新序列的樣本熵，求取其均值，得到該尺度的多尺度熵值。本文隨機選取一名健康兒童 F7 通道腦電數據的三種多尺度熵，結果如圖 4 所示。
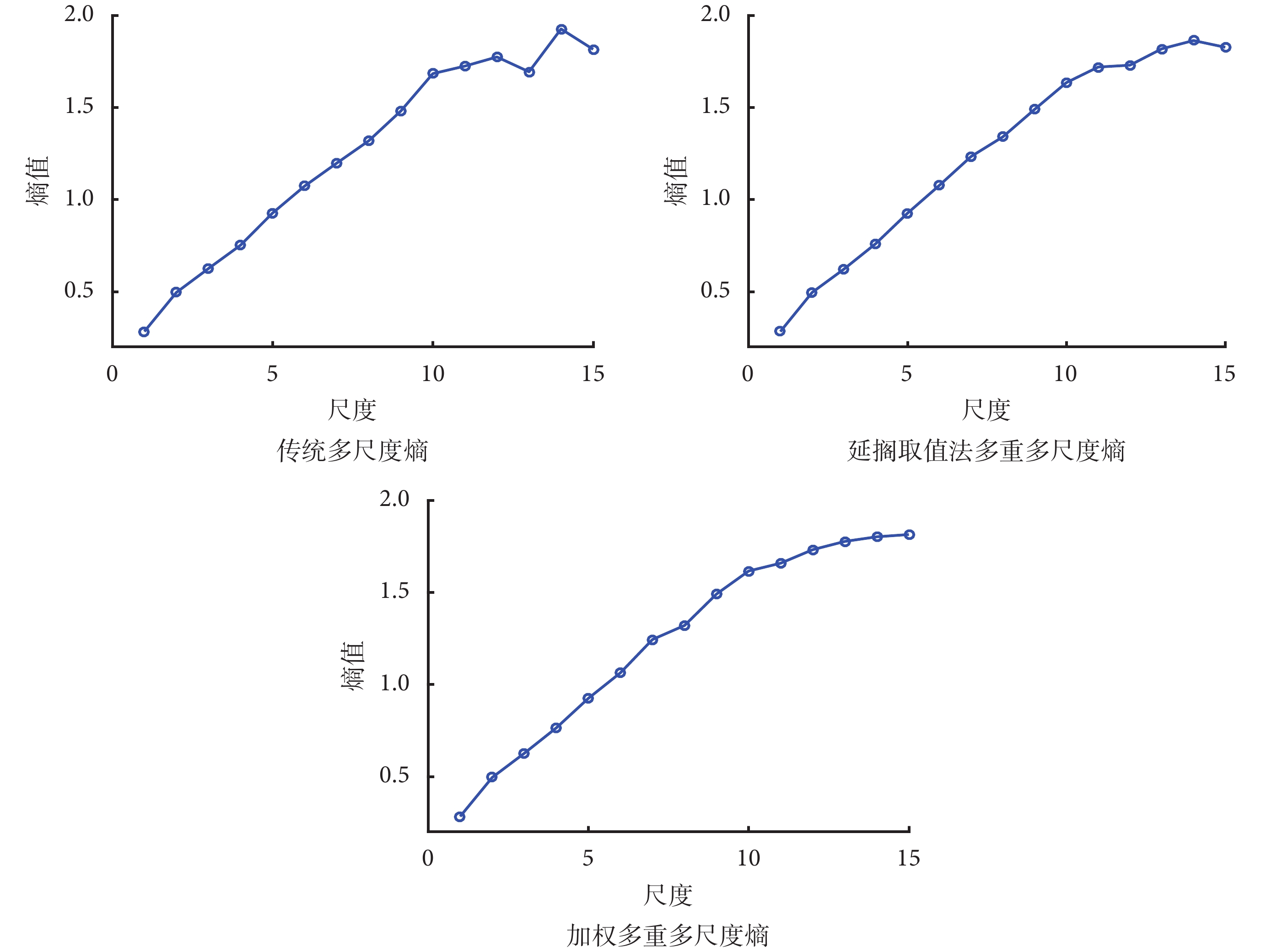圖4
F7 通道三種多尺度熵對比
Figure4.
Three multiscale entropy comparison of F7 channels
由圖 4 可知，三種多尺度熵在每個尺度的熵值大小差別不大，趨勢相同，都是隨著尺度的增大而增大。但傳統多尺度熵尺度之間的波動較大，無法體現腦電信號特征隨尺度變化的趨勢。如圖 4 中的腦電信號特征應為多尺度熵隨尺度的增大而增大，并逐漸穩定到 1.8 左右。傳統多尺度熵在尺度 13、14 波動較大，無法準確確定其穩定趨勢，而延擱取值法多重多尺度熵與加權多重多尺度熵穩定趨勢更加明顯。相比于延擱取值法在尺度 14 仍有小幅度的波動，加權多重多尺度熵則更加穩定，隨尺度變化的特征更加清晰、明顯，在信息丟失問題方面處理得更好，在處理某些精細信號方面更具優勢。
本文分別分析了 50 名受試者全部 19 通道腦電數據的樣本熵、傳統多尺度熵、延擱取值法多重多尺度熵與加權多重多尺度熵。基于支持向量機分類結合粒子群算法尋優實現分類，結果如表 1 所示。
表1
熵特征分類準確率對比
Table1.
Comparison of entropy classification accuracy
由表 1 可知，樣本熵經過粒子群尋優后的分類準確率為 58.6%，傳統多尺度熵為 71.2%，多重多尺度熵為 75.2%，而加權多重多尺度熵則是 81.6%，即加權多重多尺度熵的分類準確率最高，相比于樣本熵、傳統多尺度熵與多重多尺度熵準確率分別提高了 23.0%、10.4% 與 6.4%。由此可見，加權多重多尺度熵更能充分提取腦電信號特征。
3.3 基于加權多重多尺度熵的腦電信號分析
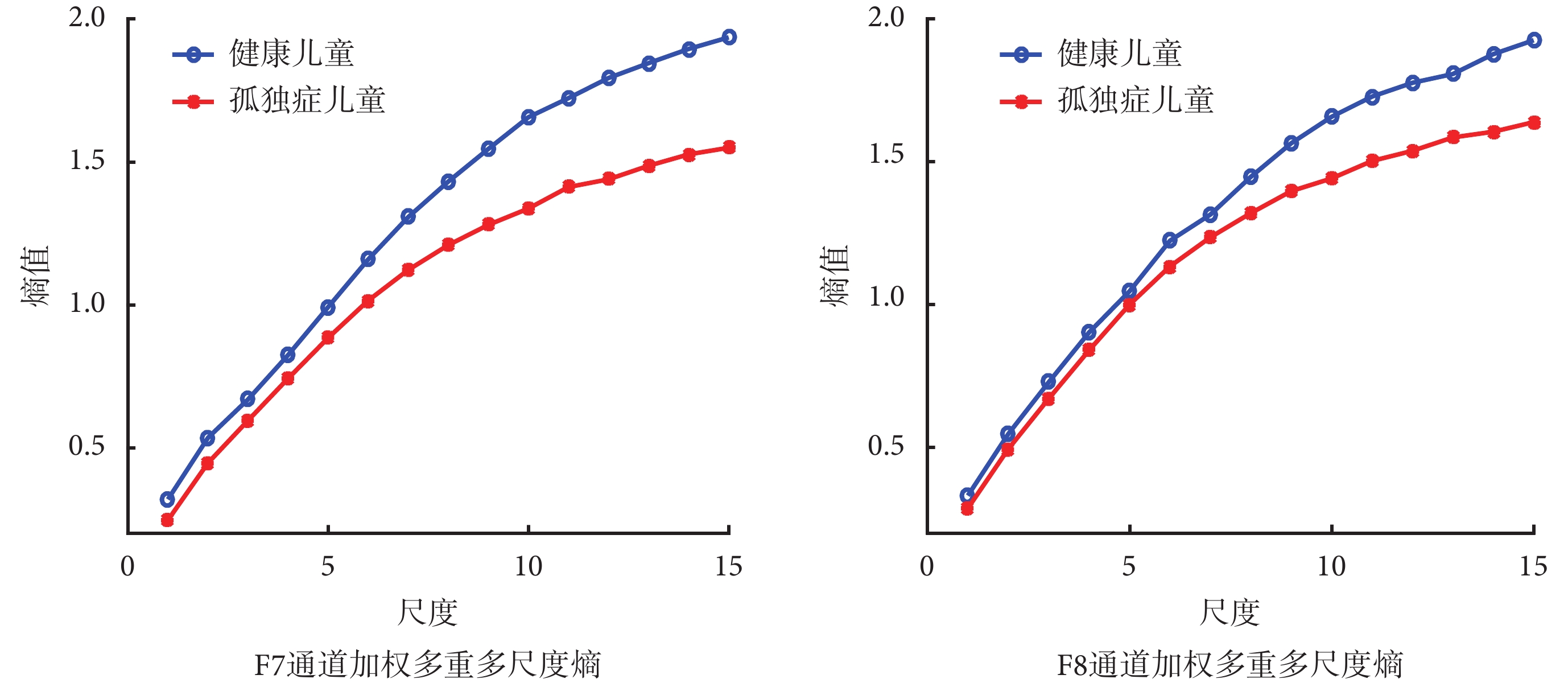
對 25 名孤獨癥兒童與 25 名健康兒童的腦電數據進行加權多重多尺度熵計算，并求取每個通道平均多尺度熵值。最終結果顯示，除通道 FP2 外，其余通道均為健康兒童的加權多重多尺度熵值略高于孤獨癥兒童，尺度越大，趨勢越為明顯。2013 年，Ecker 等[18]以孤獨癥患者與正常人群作為研究對象，探索了他們的大腦中正確連接皮層內部區域所需的連接長度，結果顯示，自閉癥患者的“連線成本”遠遠低于正常人，大腦的前顳葉區域尤甚。因此本文以前顳葉區的 F7、F8 通道為例，研究孤獨癥兒童與健康兒童的加權多重多尺度熵特征，結果如圖 5 所示。
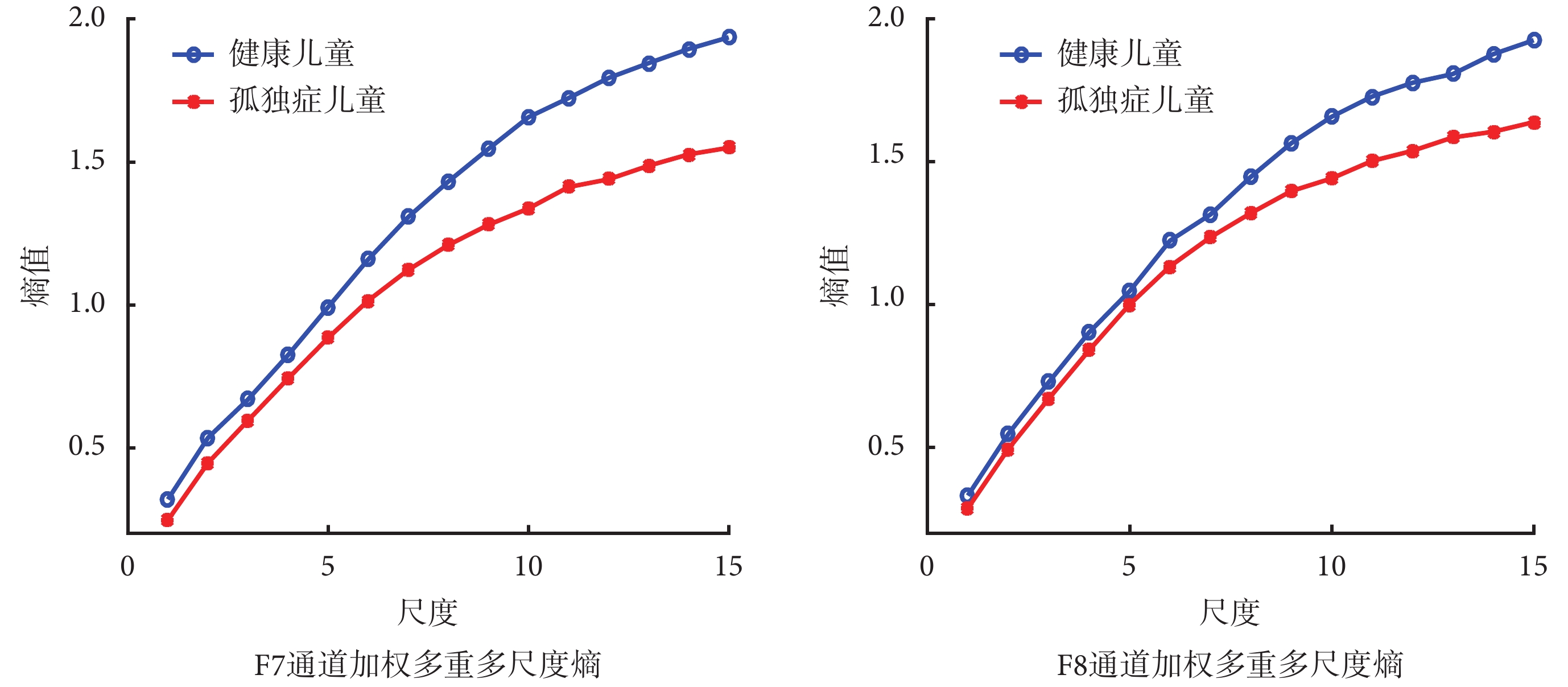圖5
F7、F8 通道加權多重多尺度熵
Figure5.
Weighted multiple multiscale entropy of F7 and F8 channels
由圖 5 可知，F7、F8 通道的加權多重多尺度熵趨勢相同，都是隨著尺度的增大而升高，健康兒童在每個尺度的加權多重多尺度熵均比孤獨癥兒童略高，尺度越大，差異越明顯。按照國際標準的 10/20 系統大腦腦區通道分布具有左右對稱性理論，去除中軸線區域單獨的 Pz、Fz 和 Oz 通道后，對成對的 16 通道加權多重多尺度熵值進行統計學顯著性檢驗，結果如表 2 所示。
表2
16 通道顯著性檢驗
Table2.
Saliency detection of 16 channels
由表 2 可知，通道 F3、F7、F8、C3、P3 加權多重多尺度熵值的差異均具有統計學意義（P<0.05），其余 11 個通道的差異不具有統計學意義（P>0.05）。由于國際標準的 10/20 系統其大腦腦區通道分布具有左右對稱性，F3、F7、F8、C3、P3 這 5 個通道，只有 F7、F8 左右對稱，可以代表前顳葉，即前顳葉的腦電數據加權多重多尺度熵在孤獨癥兒童與健康兒童之間的差異具有統計學意義（P<0.05）。以對稱的兩個通道腦電數據的加權多重多尺度熵為各個腦區的代表，對孤獨癥兒童與健康兒童進行粒子群尋優的支持向量機分類，結果如表 3 所示。
表3
各腦區加權多重多尺度熵分類準確率
Table3.
Accuracy rate of weighted multiple multiscale entropy classification in different brain regions
由表 3 可知，前顳葉的 2 個通道分類準確率最高，明顯高于其它腦區，達到了 81.2%，為前文的結果提供了有力的論證。
樣本熵能夠反映時間序列混沌程度，序列混沌程度越大，熵值越大，復雜度越高；反之，熵值越小，序列越規則，產生新模式信號的概率越小[19]。如圖 5 所示，孤獨癥兒童的多尺度熵除 FP2 通道外，其余均略小于健康兒童。正常健康兒童與孤獨癥兒童前顳葉 F7、F8 通道的腦電信號多尺度熵的差異具有統計學意義（P<0.05），因此前顳葉腦區可以作為區分孤獨癥兒童與健康兒童的一個有效腦區。
2011 年，Catarino 等[12]用多尺度熵證明了孤獨癥兒童的腦電信號復雜性低于健康兒童，同時證明孤獨癥兒童顳葉的腦電特性與健康兒童的差異具有統計學意義。而 Jaime 等[20]通過相干函數計算孤獨癥患者腦電信號，發現孤獨癥患者右腦顳葉中部的相干性低于健康人。Sheikhani 等[21]通過研究靜息態腦電信號發現，孤獨癥兒童顳區（T 區）Gamma 頻段的腦電信號相干性顯著升高。Greimel 等[22]和 Ecker 等[23]更是直接指出孤獨癥患者的敏感腦區位于顳葉與頂葉。基于以上研究，本文以加權多重多尺度熵研究孤獨癥兒童與健康兒童的腦電信號特征的差異，同樣確定前顳葉是孤獨癥的一個敏感腦區。
4 結論
本文針對傳統多尺度熵存在的信息丟失問題，提出了一種加權多重多尺度熵算法。該算法基于經驗模態分解過程中通過分解原始序列得到多個本征模函數分量的思想，在每個尺度構建幅值從大到小的多重序列并結合相關系數，計算每重序列相關系數在總相關系數中所占的比重，作為相關權重計算加權多重多尺度熵，充分考慮了各序列的相關貢獻度，加強了各序列與該尺度加權多重多尺度熵的相關關系，從而克服了傳統多尺度熵信息丟失的問題，使熵特征值變化趨勢更加平穩，在挖掘信號隱藏的細節信息方面更具優勢。本文通過比較樣本熵、傳統多尺度熵、延擱取值法多重多尺度熵與加權多重多尺度熵特征分類準確率發現：加權多重多尺度熵的分類準確率最高，相比于樣本熵、傳統多尺度熵與延擱取值法多重多尺度熵的分類準確率分別提高了 23.0%、10.4% 與 6.4%，表明加權多重多尺度熵能更充分地提取腦電信號特征，是一種更有優勢的腦電信號特征提取算法。
本文用加權多重多尺度熵腦電信號特征提取算法，以獨孤癥兒童腦電信號為對象，提取孤獨癥兒童與健康兒童 19 個通道腦電信號特征。最終研究結果顯示，除 FP2 通道外，其余 18 個通道的加權多重多尺度熵值均為健康兒童高于孤獨癥兒童，F3、F7、F8、C3、P3 這 5 個通道的差異具有統計學意義（P<0.05）。在此基礎上，本文進一步比較孤獨癥兒童與健康兒童各個腦區的加權多重多尺度熵分類準確率，結果發現：前顳葉（F7、F8）的準確率最高，達到了 81.2%。由此可知，前顳葉可以作為分析孤獨癥兒童腦功能狀態的敏感腦區。分析前顳葉區域的腦電信號特性可以為孤獨癥兒童腦功能狀態的評估提供有效的幫助。
引言
孤獨癥，也稱自閉癥，是一種起源于兒童早期，以社會交往和溝通障礙、興趣范圍狹窄及重復刻板行為為主要特征的廣泛性發育障礙[1-2]。據 2015 年調查數據顯示，孤獨癥發病率已經達到了 1∶45[3]。
國內對孤獨癥研究從最初的心理學和行為學研究，逐漸向腦功能電生理分析和影像學研究方向發展。腦電信號通過記錄大腦皮層的電生理活動，能夠表現出大腦的神經系統內部活動[4]。Duffy 等[5]通過大量的研究，發現了一種穩定的腦電譜耦合模式，可以有效地識別孤獨癥兒童。Dawson 等[6]比較了孤獨癥兒童和對照組兒童的腦電信號功率譜，該項研究結果表明，相對于對照組兒童，孤獨癥兒童在前額和顳區的腦電信號功率譜偏低，左半球比右半球更加明顯。Pineda 等[7]通過神經反饋訓練發現，經過訓練的孤獨癥患者 mu 頻帶（10～13 Hz）功率和相干性降低。由此可見，腦電信號分析是研究孤獨癥兒童腦功能狀態的一種有效方法。
腦電信號具有非線性和非平穩性的特點[8]。常用的腦電信號非線性分析方法主要有：經驗模態分解（empirical mode decomposition，EMD）算法和赫斯特（Hurst）指數分析等[9]。熵算法能夠刻畫系統所處狀態的無序性和混亂程度，有助于更深入地理解腦電信號中的動態變化以及大腦中潛在的混沌狀態，且與其他非線性方法相比，熵具有對數據長度依賴更小的優點[10]。Srinivasan 等[11]采用近似熵（approximate entropy，ApEn）提取腦電信號中的特征，基于概率神經網絡（probabilistic neural network，PNN）對腦電數據進行分類，得到了 84.5% 的準確率。Catarino 等[12]基于多尺度熵（multiscale entropy，MSE）的方法提取孤獨癥兒童腦電信號特征，結果表明孤獨癥患者的腦電復雜度（complexity，CPX）明顯降低。
多尺度熵特征提取算法能夠充分挖掘腦電信號隱藏的細節信息。Bornas 等[13]和 Thuraisingham 等[14]證明了在反映腦電信號特征方面，多尺度熵算法能夠提取到更多的細節信息。Li 等[15]將多尺度熵算法與排序熵（permutation entropy，PE）結合，克服了排序熵的不足，更好地描述了腦電信號特性，同時證明多尺度排序熵在腦電信號分析中更有優勢。
本文針對傳統多尺度熵在多尺度化過程中，因序列縮短而造成的信息丟失問題，提出一種加權多重多尺度熵特征提取方法。該算法基于經驗模態分解多尺度分解思想，考慮到對每個數據的充分利用，且不改變原始序列的波動形式，加權多重多尺度熵在每個尺度上以尺度為時間窗參數，構建等長的時間窗，依次從每個時間窗提取從大到小的數據點，構建多重數據序列。將該尺度均值粗粒化（coarse graining，CG）后的序列作為基點，計算該序列與多重序列的相關系數，進一步計算每重序列相關系數占該尺度多重序列總相關系數的比重，作為相關權重，再運用加權理論計算每個尺度的總樣本熵。相比于傳統多尺度熵在每個尺度構建一個序列，以及單一多重多尺度熵認為多重序列貢獻率相同的簡單處理方法，基于加權多重多尺度熵特征提取算法不但克服了信息丟失問題，還充分考慮了多重序列間的相關性與對總熵值的貢獻程度，減小了尺度間的波動，更能挖掘腦電信號的細節信息。
基于加權多重多尺度熵算法，本文對孤獨癥兒童和健康對照組兒童靜息態腦電信號進行特征提取，通過分析孤獨癥兒童和健康兒童 19 通道的加權多重多尺度熵，結合統計產品與服務解決方案（statistical product and service solutions，SPSS）軟件數據分析和支持向量機（support vector machine，SVM）的分類，探究孤獨癥兒童與健康兒童腦電數據復雜性的差異，由此探究孤獨癥兒童的異常通道，定位其敏感腦區，為孤獨癥兒童的腦功能狀態評估與分析提供一種有效的新方法。
1 加權多重多尺度樣本熵
1.1 樣本熵
樣本熵（sample entropy，SampEn）（以符號 SampEn 表示）是一種衡量時間序列復雜度的方法，是對近似熵算法的改進[16]。對于給定的時間序列{x1，x2，，xi，，xN}，構建一個 m 維的矢量，如式（1）所示：
|
定義 d ［xi，xj］為兩個矢量元素 xi 和 xj 之間的最大距離，如式（2）所示：
|
然后，定義閾值 r，統計 d［xi，xj］小于閾值 r 的數目 n，計算 n 與 d［xi，xj］數目的比值，記為 Cim（r），如式（3）所示：
|
N ? m 是 d［xi，xj］的總元素數量。如式（4）所示，可得到所有 Cim（r）的平均值 Cm（r）：
|
在此基礎上，將維數加 1，使之變為 m+1 維的矢量，重復上述步驟得到 Cm+1（r）。然后，計算該尺度樣本熵值，如式（5）所示：
|
其中，m 是嵌入維數，r 是閾值。
1.2 加權多重多尺度樣本熵
加權多重多尺度熵算法針對傳統多尺度熵隨著尺度增大而使數據序列縮短所造成的信息丟失問題，基于經驗模態分解中多尺度分解思想，在每個尺度構建多重序列，考慮每重序列的相關貢獻程度，運用加權理論，計算每個尺度的總樣本熵，最大程度地克服了信息丟失問題。加權多重多尺度熵算法的具體步驟如下：
（1）對于給定的時間序列{u1，u2，，ui，，uN}，構建各尺度多重序列，步驟如圖 1 所示。每個尺度構建 s 個新序列。即當 s = 1 時，新序列只有一個，而 s1 時，該尺度下的新序列有 s 個。如圖 2 所示為尺度為 5 時傳統多尺度熵單重序列與加權多重多尺度熵多重序列的對比。由圖 2 可知，在尺度為 5 時，傳統多尺度熵只構建了單重數據序列，而加權多重多尺度熵則構建了與尺度相等的五重數據序列，每重序列的波動形式與傳統多尺度熵的單重序列一致，且五重序列按幅值從大到小排列。加權多重多尺度熵構建多重序列，通過增加重構的序列數量，可以避免傳統多尺度熵的信息丟失問題。
圖1
多重序列構建
Figure1.
Multiple sequence construction
圖2
尺度為 5 時序列對比
Figure2.
Comparison of sequences with scale of 5
（2）然后，計算每重序列在該尺度下的比重：對于給定的時間序列{u1，u2，，ui，，uN}，進行均值粗粒化處理，得到每個尺度下的新序列 Q（s）。以新序列 Q（s） 為基點，計算步驟（1）中的每個尺度下多重序列的相關系數[17]，如式（6）所示：
|
（3）進一步計算每個序列在該尺度下所占的權重 w，如式（7）所示：
|
（4）再進一步計算多重序列的樣本熵，如式（8）所示：
|
（5）最后計算該尺度下的樣本熵（以符號 qSampEn 表示），如式（9）所示：
|
2 腦電數據采集及預處理
2.1 腦電數據采集
本試驗采用 128 導聯腦電圖分析系統（Net Station4.5.2，Electrical Geodesics Inc，美國）進行時長 5 min 的靜息態腦電信號采集。按照國際標準的 10/20 系統將 Cz 電極作為參考，同時設置每個電極小于 50 kΩ 的阻抗值，參考電極和雙側乳突處的電極阻抗值則小于 10 kΩ，采樣率為 1 000 Hz。
本文共招募了 50 名兒童受試者，其中 25 名孤獨癥兒童（試驗組）與 25 名健康兒童（對照組）。試驗組兒童，年齡范圍在 4～8 歲，平均年齡為（6.30±1.43）歲；對照組兒童，年齡范圍在 4～8 歲，平均年齡為（6.43±1.27）歲。試驗前，要求受試者靜息 2 min，以便受試者進入放松狀態。試驗過程在安靜的房間中進行，期間保持安靜狀態，盡可能避免或減小外界干擾。本試驗所有受試人員及其家長均簽署了知情同意書。
2.2 腦電數據預處理
數據預處理步驟如下：
（1）壞通道替換，將有問題通道的數據由周圍通道數據均值進行替換。
（2）從 128 個通道中按照國際標準的 10/20 系統選出 19 個通道，分別位于額葉、頂葉、枕葉、左顳葉和右顳葉等 5 個腦區，如圖 3 所示。
圖3
19 通道腦區分布圖
Figure3.
Brain distribution map of 19 channels
（3）去除眨眼、眼動、呼吸偽跡、工頻干擾、肌電、心電、突變斜坡和離群值等偽跡信號，進行 0.5～45.0 Hz 的帶通濾波。
3 腦電數據處理結果與分析
3.1 多尺度參數設置
根據以往的研究，嵌入維數 m 設置為 2，閾值設置為 r = 0.15 × std（x），其中 std（x）為時間序列 x 的標準差。最大尺度 s 設置為 15，這樣就不會由于尺度過小而使特征體現不出明顯的趨勢，也不會因為尺度過大而造成計算復雜的問題。
3.2 多尺度熵對比分析
對比分析 25 名孤獨癥兒童與 25 名健康兒童腦電信號特征參數，分別提取傳統多尺度樣本熵、延擱取值法多重多尺度樣本熵與加權多重多尺度樣本熵特征量。所謂延擱取值法多重多尺度熵是對傳統多尺度熵算法的一種改進，即在移動均值粗粒化（moving averaging，MA）的基礎上，運用延擱取值法在每個尺度上構建多重數列，即由第一個數據點開始，相隔相關尺度個數據點依次取值，從而構建多重數列，再求取多重數列的樣本熵均值作為該尺度的樣本熵值。延擱取值法多重多尺度熵具體算法步驟如下：
（1）對給定的時間序列{x1，x2，，xi，，xN}，以尺度為 s 進行移動均值粗粒化，得到新序列 Z（s），長度為 N ? s + 1。再對新序列 Z（s）以尺度為 s 為參數進行延擱法取值，構建多重序列 V（s），長度為 l。如式（10）、（11）所示：
|
|
最后計算每個尺度構建的多重新序列的樣本熵，求取其均值，得到該尺度的多尺度熵值。本文隨機選取一名健康兒童 F7 通道腦電數據的三種多尺度熵，結果如圖 4 所示。
圖4
F7 通道三種多尺度熵對比
Figure4.
Three multiscale entropy comparison of F7 channels
由圖 4 可知，三種多尺度熵在每個尺度的熵值大小差別不大，趨勢相同，都是隨著尺度的增大而增大。但傳統多尺度熵尺度之間的波動較大，無法體現腦電信號特征隨尺度變化的趨勢。如圖 4 中的腦電信號特征應為多尺度熵隨尺度的增大而增大，并逐漸穩定到 1.8 左右。傳統多尺度熵在尺度 13、14 波動較大，無法準確確定其穩定趨勢，而延擱取值法多重多尺度熵與加權多重多尺度熵穩定趨勢更加明顯。相比于延擱取值法在尺度 14 仍有小幅度的波動，加權多重多尺度熵則更加穩定，隨尺度變化的特征更加清晰、明顯，在信息丟失問題方面處理得更好，在處理某些精細信號方面更具優勢。
本文分別分析了 50 名受試者全部 19 通道腦電數據的樣本熵、傳統多尺度熵、延擱取值法多重多尺度熵與加權多重多尺度熵。基于支持向量機分類結合粒子群算法尋優實現分類，結果如表 1 所示。
表1
熵特征分類準確率對比
Table1.
Comparison of entropy classification accuracy
由表 1 可知，樣本熵經過粒子群尋優后的分類準確率為 58.6%，傳統多尺度熵為 71.2%，多重多尺度熵為 75.2%，而加權多重多尺度熵則是 81.6%，即加權多重多尺度熵的分類準確率最高，相比于樣本熵、傳統多尺度熵與多重多尺度熵準確率分別提高了 23.0%、10.4% 與 6.4%。由此可見，加權多重多尺度熵更能充分提取腦電信號特征。
3.3 基于加權多重多尺度熵的腦電信號分析
對 25 名孤獨癥兒童與 25 名健康兒童的腦電數據進行加權多重多尺度熵計算，并求取每個通道平均多尺度熵值。最終結果顯示，除通道 FP2 外，其余通道均為健康兒童的加權多重多尺度熵值略高于孤獨癥兒童，尺度越大，趨勢越為明顯。2013 年，Ecker 等[18]以孤獨癥患者與正常人群作為研究對象，探索了他們的大腦中正確連接皮層內部區域所需的連接長度，結果顯示，自閉癥患者的“連線成本”遠遠低于正常人，大腦的前顳葉區域尤甚。因此本文以前顳葉區的 F7、F8 通道為例，研究孤獨癥兒童與健康兒童的加權多重多尺度熵特征，結果如圖 5 所示。
圖5
F7、F8 通道加權多重多尺度熵
Figure5.
Weighted multiple multiscale entropy of F7 and F8 channels
由圖 5 可知，F7、F8 通道的加權多重多尺度熵趨勢相同，都是隨著尺度的增大而升高，健康兒童在每個尺度的加權多重多尺度熵均比孤獨癥兒童略高，尺度越大，差異越明顯。按照國際標準的 10/20 系統大腦腦區通道分布具有左右對稱性理論，去除中軸線區域單獨的 Pz、Fz 和 Oz 通道后，對成對的 16 通道加權多重多尺度熵值進行統計學顯著性檢驗，結果如表 2 所示。
表2
16 通道顯著性檢驗
Table2.
Saliency detection of 16 channels
由表 2 可知，通道 F3、F7、F8、C3、P3 加權多重多尺度熵值的差異均具有統計學意義（P<0.05），其余 11 個通道的差異不具有統計學意義（P>0.05）。由于國際標準的 10/20 系統其大腦腦區通道分布具有左右對稱性，F3、F7、F8、C3、P3 這 5 個通道，只有 F7、F8 左右對稱，可以代表前顳葉，即前顳葉的腦電數據加權多重多尺度熵在孤獨癥兒童與健康兒童之間的差異具有統計學意義（P<0.05）。以對稱的兩個通道腦電數據的加權多重多尺度熵為各個腦區的代表，對孤獨癥兒童與健康兒童進行粒子群尋優的支持向量機分類，結果如表 3 所示。
表3
各腦區加權多重多尺度熵分類準確率
Table3.
Accuracy rate of weighted multiple multiscale entropy classification in different brain regions
由表 3 可知，前顳葉的 2 個通道分類準確率最高，明顯高于其它腦區，達到了 81.2%，為前文的結果提供了有力的論證。
樣本熵能夠反映時間序列混沌程度，序列混沌程度越大，熵值越大，復雜度越高；反之，熵值越小，序列越規則，產生新模式信號的概率越小[19]。如圖 5 所示，孤獨癥兒童的多尺度熵除 FP2 通道外，其余均略小于健康兒童。正常健康兒童與孤獨癥兒童前顳葉 F7、F8 通道的腦電信號多尺度熵的差異具有統計學意義（P<0.05），因此前顳葉腦區可以作為區分孤獨癥兒童與健康兒童的一個有效腦區。
2011 年，Catarino 等[12]用多尺度熵證明了孤獨癥兒童的腦電信號復雜性低于健康兒童，同時證明孤獨癥兒童顳葉的腦電特性與健康兒童的差異具有統計學意義。而 Jaime 等[20]通過相干函數計算孤獨癥患者腦電信號，發現孤獨癥患者右腦顳葉中部的相干性低于健康人。Sheikhani 等[21]通過研究靜息態腦電信號發現，孤獨癥兒童顳區（T 區）Gamma 頻段的腦電信號相干性顯著升高。Greimel 等[22]和 Ecker 等[23]更是直接指出孤獨癥患者的敏感腦區位于顳葉與頂葉。基于以上研究，本文以加權多重多尺度熵研究孤獨癥兒童與健康兒童的腦電信號特征的差異，同樣確定前顳葉是孤獨癥的一個敏感腦區。
4 結論
本文針對傳統多尺度熵存在的信息丟失問題，提出了一種加權多重多尺度熵算法。該算法基于經驗模態分解過程中通過分解原始序列得到多個本征模函數分量的思想，在每個尺度構建幅值從大到小的多重序列并結合相關系數，計算每重序列相關系數在總相關系數中所占的比重，作為相關權重計算加權多重多尺度熵，充分考慮了各序列的相關貢獻度，加強了各序列與該尺度加權多重多尺度熵的相關關系，從而克服了傳統多尺度熵信息丟失的問題，使熵特征值變化趨勢更加平穩，在挖掘信號隱藏的細節信息方面更具優勢。本文通過比較樣本熵、傳統多尺度熵、延擱取值法多重多尺度熵與加權多重多尺度熵特征分類準確率發現：加權多重多尺度熵的分類準確率最高，相比于樣本熵、傳統多尺度熵與延擱取值法多重多尺度熵的分類準確率分別提高了 23.0%、10.4% 與 6.4%，表明加權多重多尺度熵能更充分地提取腦電信號特征，是一種更有優勢的腦電信號特征提取算法。
本文用加權多重多尺度熵腦電信號特征提取算法，以獨孤癥兒童腦電信號為對象，提取孤獨癥兒童與健康兒童 19 個通道腦電信號特征。最終研究結果顯示，除 FP2 通道外，其余 18 個通道的加權多重多尺度熵值均為健康兒童高于孤獨癥兒童，F3、F7、F8、C3、P3 這 5 個通道的差異具有統計學意義（P<0.05）。在此基礎上，本文進一步比較孤獨癥兒童與健康兒童各個腦區的加權多重多尺度熵分類準確率，結果發現：前顳葉（F7、F8）的準確率最高，達到了 81.2%。由此可知，前顳葉可以作為分析孤獨癥兒童腦功能狀態的敏感腦區。分析前顳葉區域的腦電信號特性可以為孤獨癥兒童腦功能狀態的評估提供有效的幫助。
