腦機接口(BCI)系統通過從腦信號中提取特征對其進行識別。針對自回歸模型特征提取方法和傳統主成分分析降維方法處理多通道信號的局限性, 本文提出了多變量自回歸(MVAR)模型和多線性主成分分析(MPCA)結合的多通道特征提取方法, 并用于腦磁圖/腦電圖(MEG/EEG)信號識別。首先計算MEG/EEG信號的MVAR模型的系數矩陣, 然后采用MPCA對系數矩陣進行降維, 最后使用線性判別分析分類器對腦信號分類。創新在于將傳統單通道特征提取方法擴展到多通道。選用BCI競賽IV數據集3和1數據進行實驗驗證, 兩組實驗結果表明MVAR和MPCA結合的特征提取方法處理多通道信號是可行的。
引用本文: 王金甲, 張彥娜. 多變量自回歸和多線性主成分分析結合的多通道信號特征提取研究. 生物醫學工程學雜志, 2015, 32(1): 19-24. doi: 10.7507/1001-5515.20150004 復制
引言
腦機接口(brain-computer interface,BCI)依賴人的意識通過腦信號來對計算機或其他的外部設備進行控制[1]。如何提高腦電圖(electroencephalograph, EEG)和腦磁圖(magnetoencephalography, MEG)信號的識別性能仍是BCI研究中的關鍵問題[1]。目前腦信號的特征提取方法主要包括:小波包分解、自回歸(autoregression,AR)模型參數估計、時頻分析、相關性分析、共空間模式(common spatial patterns,CSP)等[2],其中AR模型在腦信號研究中應用廣泛。Lawhern等[3]采用AR模型對含有不同偽跡的連續EEG進行特征提取和分類。Keirn等[4]對每個通道EEG信號建立AR模型,將6個通道的AR模型系數連接起來作為特征進行分類。一般AR模型只適用于單通道信號,處理多通道EEG信號時存在局限性,例如忽略各個通道間相互作用。因此針對多通道信號建立的多變量自回歸(multivariate autoregressive,MVAR)模型更適合用于腦信號的研究[5]。薛建中等[6]給出了MVAR模型和核主成分分析降維方法結合方法并用于EEG信號識別。王江等[7]研究了MUAR模型算法并用于EEG信號特征提取。Zhao等[8]研究將EEG信號MVAR模型用于駕駛精神疲勞狀態的檢測。王寧等[9]研究了EEG信號MVAR模型用于情緒認知。除此之外MVAR模型在心電、肌電等信號的特征提取和分類等方面都有應用。Anderson等[10]對兩個意識任務、6個通道EEG信號進行了單變量和多變量AR模型特征提取的對比研究,結果表明MVAR模型系數作為特征能夠獲得更好的識別率。但是多通道腦信號通過建立MVAR模型求得的系數是矩陣,轉化為向量特征時會產生高維小樣本問題。
本文對多通道MEG/EEG信號建立MVAR模型,采用文獻[11]的歸一化LWR算法估計的MVAR模型系數矩陣作為特征。為了考慮系數矩陣的關聯性,提出采用多線性主成分分析(multilinear principal component analysis,MPCA)[12]對系數矩陣直接進行降維,而無需轉化為向量特征進行降維。最后分類器采用線性判別分析。新方法在BCI競賽Ⅳ的數據集3和1的實驗結果說明利用多通道信號處理方法提取MEG/EEG信號特征是可行的。
1 MVAR算法
由于腦信號是典型的多通道信號,因此首先建立腦信號的MVAR模型,然后給出求解MVAR系數矩陣的方法。
1.1 MVAR模型介紹
模型階數為m的d變量AR模型可以表示為
| $ \boldsymbol{X}(n)=\sum\limits_{i=1}^{m}{\boldsymbol{A} \left(i \right)}X\left(n-i \right)+\boldsymbol{E} \left(n \right) $ |
其中X(n)=(xi(n), …, xd(n))T是(d×1)的列向量,E(n)是(d×1)的激勵噪聲向量,n=0, …, N-1表示時間采樣點數,模型參數A(i)(i=1, 2, …, m)是(d×d)的預測系數矩陣,元素auv(i),u, v=1, …, d表示xv(n-i)對xu(i)的線性關聯作用,并且當u≠v時,auv≠avu。
1.2 MVAR模型系數矩陣求解
定義前、后向預測均方誤差分別為RmF=A m(i)R(-i)、R mG=Bm(i)R(i),A m(i)、B m(i)分別是m階前、后向預測第i個系數矩陣,前、后向預測均方誤差Δm=Am-1(i)R(m-i),其中自相關函數R(k)=E{ X(n)X(n-k)T}由樣本{X(0), X(2),…,X(N-1)}估計,即。
基于歸一化LWR算法求解M階MVAR模型系數的具體過程如下:
輸入:X(n), n=0, …, N-1,并設置R0G=P0=Q0=R0=R(0)=X(n)X(n)T,?0(0)= 0(0)=(R0G)-1/2, m=1
輸出:MVAR模型系數矩陣A
(1)計算前、后向均方誤差:m=?m-1(0)R(m)+?m-1(1)R(m-1)+…+? m-1(m-1)R(1)
(2)計算反射系數等中間變量值:ρm=m(Rm-1G)-T/2,Pm=Ⅰ-ρmρmT,Qm=Ⅰ-ρmTρm,(RmG)-1/2(Rm-1G)-1/2
(3)計算模型系數,其中k的取值從0~m
| $ \begin{align} & {{{\tilde{A}}}_{m}}\left(k \right)=P_{m}^{-1/2}\left[{{{\tilde{A}}}_{m-1}}\left(k \right)-{{\rho }_{m}}{{{\tilde{B}}}_{m-1}}\left(k \right)\right] \\ & {{{\tilde{B}}}_{m}}\left(k \right)=Q_{m}^{-1/2}\left[{{{\tilde{B}}}_{m-1}}\left(k \right)-\rho _{^{m}}^{T}{{{\tilde{A}}}_{m-1}}\left(k \right)\right] \\ \end{align} $ |
(4)當m<M時,令m=m+1,返回步驟(1)執行;當m=M時,輸出系數A(k)。
1.3 噪聲協方差矩陣的討論
預測均方誤差矩陣即模型中的噪聲源協方差矩陣,如果通道間激勵噪聲源相互獨立,則預測均方誤差是對角矩陣。然而實際中不同通道間的激勵噪聲源是相關的,所以其預測誤差是非對角矩陣。噪聲源的相關性對預測變量的影響可以通過模型系數的變化來體現,使得估計的系數更準確表示預測信號。這一思想可以通過以下變換來實現RMF=b Rdlag b *,其中b是通過對噪聲協方差矩陣進行Cholesky分解得到的下三角矩陣。因此MVAR模型的系數可以重新表示為Anew(k)=b -1A(k),k=0, …,m。
2 MPCA特征降維
對d通道信號建立m階MVAR模型,模型系數的數目為(d×d×m)。假設通道數為10,階數為6,則總數目共有600個,所以有必要進行特征降維處理以消除大量冗余特征。多通道腦信號通過建立MVAR模型求得的系數是矩陣形式,為了考慮系數矩陣的關聯性,提出采用MPCA方法對系數矩陣直接進行降維。
MPCA定義為張量空間RI1?RI2…?RIN'到張量子空間RP1?RP2…?RIN'的多線性變換[12],要求子空間維數Pn′小于原空間維數In′,當Pn′=In′時為全投影。投影公式為
| $ {{y}_{{{m}^{'}}}}={{x}_{{{m}^{'}}}}{{\text{ }\!\!\times\!\!\text{ }}_{1}}{{\widetilde{\boldsymbol{\text{U}}}}^{\left( 1 \right)T}}{{\text{ }\!\!\times\!\!\text{ }}_{2}}{{\widetilde{\boldsymbol{\text{U}}}}^{\left( 1 \right)T}}\cdots {{\text{ }\!\!\times\!\!\text{ }}_{N'}}{{\widetilde{\boldsymbol{\text{U}}}}^{\left( {{N}^{'}} \right)T}},{{m}^{'}}=1,\cdots ,{{M}^{'}},\ \ \ \ \sum\limits_{{{i}_{n'}}=1}^{{{p}_{n'}}}{\lambda _{{{i}_{n}}}^{\left( {{n}^{'}} \right)*}}/\sum\limits_{{{i}_{n'}}=1}^{{{I}_{n'}}}{\lambda _{{{i}_{{{n}^{'}}}}}^{\left( n \right)*}} $ |
其中M′為張量樣本的個數,N′為張量階數,滿足N′≥1。比率Q(n′)=表示n′階張量投影后保留的特征比例,λ(n′)*in′是第in′個全投影矩陣的n′階特征值。
是MPCA算法的目標函數最優化的解,即{∈RIN'×Pn′, n′=1, …, N′}為投影矩陣。
3 MVAR和MPCA結合的特征提取和分類方法
MVAR模型和MPCA結合的腦信號多通道特征提取方法簡要敘述如下:首先將多通道腦信號建立MVAR模型,用歸一化LWR算法求解模型系數。然后將訓練數據模型系數矩陣作零均值處理,求出對應的全投影矩陣,對其進行矩陣特征分解,確定子空間維數后,結合得到的特征向量和比率Q(n′),求得投影矩陣。最后將訓練和測試數據的模型系數矩陣投影到矩陣上,達到降維目的。
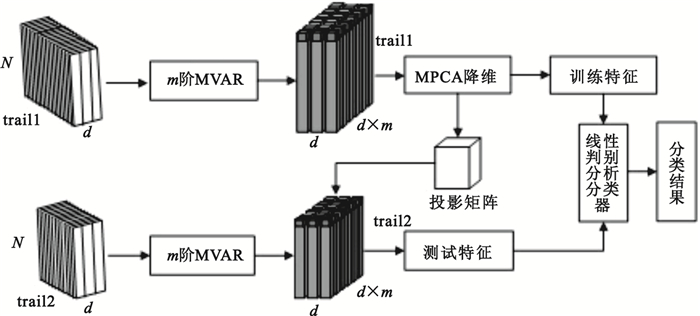
MVAR和MPCA結合的腦信號特征提取和分類過程如圖 1所示。圖中trail1、trail2分別表示受試者進行訓練實驗和測試實驗的次數,每次實驗采集腦信號的數據格式為N×d,N為采樣點數,d為通道數,m為MVAR模型的階數,圖中假設d=3,m=2。
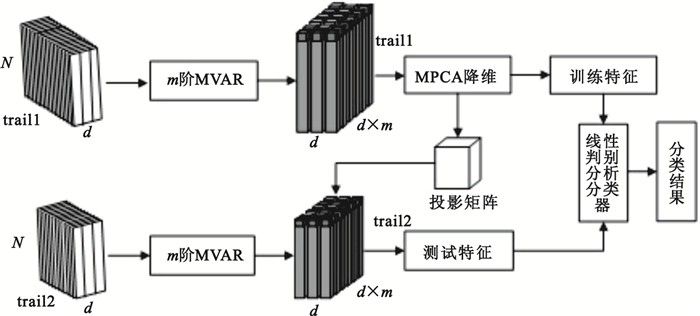 圖1
MVAR和MPCA結合的腦信號特征提取和分類示意圖
Figure1.
Diagram of brain signal feature extraction and classification based on MVAR combined with MPCA
圖1
MVAR和MPCA結合的腦信號特征提取和分類示意圖
Figure1.
Diagram of brain signal feature extraction and classification based on MVAR combined with MPCA
整個腦信號特征提取和分類實驗過程如下:
(1)分別對單次trail的訓練數據和測試數據(數據格式為N×d)建立m階MVAR模型,最后得到數據格式為trail×d×(d×m)的系數特征張量,可以看做是3階張量。
(2)訓練數據的系數特征張量經過MPCA特征降維,得到訓練特征,并且得到投影矩陣。
(3)測試數據得到的系數特征張量在投影矩陣上投影,得到測試特征。
(4)將降維后的訓練特征改寫成向量形式,訓練線性判別分析分類器。
(5)將測試特征改寫成向量形式,送進分類器得到分類結果。
4 實驗分析
文中采用BCI CompetitionⅣ:data sets 3和data sets 1數據,實驗數據來自http://www.bbci.de/competition/。
4.1 數據介紹
實驗數據一:BCI CompetitionⅣ:data sets 3包含兩個受試者S1和S2的10通道400個采樣點的前、后、左、右4類MEG信號,數據格式表示為:實驗次數×時間采樣點數×通道數。因此,S1和S2的訓練數據分別為160×400×10和160×400×10,測試數據分別為74×400×10和73×400×10。
實驗數據二:BCI CompetitionⅣ:data sets 1包含多個健康受試者運動想象任務的59通道100個采樣點的2類EEG信號。本文實驗選擇與參考文獻[13]相同的11個通道EEG信號進行實驗,并選擇b和f受試者數據進行實驗,b和f受試者的訓練集數據格式為140×100×11,測試集數據格式為60×100×11。
4.2 實驗參數介紹
Q表示投影后在子空間中保存原始維數的比例,實驗中選擇95%~100%。
m表示MVAR模型的階數,實驗一階數選取3~7階,實驗二階數選取2~6階。
4.3 實驗結果分析
4.3.1 實驗數據一的結果
表 1為S1、S2在不同實驗參數下的識別正確率。可以看出,S1最高識別正確率為41.89%,此時MVAR模型階數為3,Q為98%。S2最高識別正確率為45.21%,此時MVAR模型階數為6,Q為100%。由實驗結果可知,MVAR系數矩陣進行MPCA降維能夠得到較好實驗結果。
表 2為本文方法與競賽前三名以及文獻[14]中多類別廣義核CSP(MGKCSP)方法和多類CSP(MCSP)方法測試集識別正確率的比較。可以知道,我們采用的MVAR模型系數作為特征并進行MPCA特征降維的方法,平均值超過MGKCSP方法12%,超過MCSP方法1.4%,超過第二名將近18%,超過第三名將近20%,具有絕對性的優勢。第二名和第三名都是采用時域或頻域特征,而MVAR方法也是采用時域或頻域特征,但效果明顯更好。MGKCSP方法和MCSP方法采用空域特征,MVAR方法優于MGKCSP方法,與MCSP方法相當。與第一名相比,雖然S1的正確率不高,但是平均值差僅差約3.4%。而S2的正確率為45.2%,超出第一名10.9%,超出MCSP方法9.6%。對于S2測試數據識別正確率的實驗,相關文獻的實驗結果都不好,而本文卻得出45.2%的優異結果。這說明采用MVAR模型系數作為特征,并且結合MPCA特征降維方法對于S1和S2分類具有很好的穩定性,新方法適合處理多通道MEG信號,應該很有推廣的價值。
4.3.2 實驗數據二的結果
表 3為b、f在不同實驗參數下的識別正確率,表示10次測試集分類正確率的均值和標準差。可以看出,MVAR模型的階數為2,Q為100%時,b的最高識別正確率均值為69.3%,標準差為3.6%;f的最高識別正確率均值為82.8%,標準差為3.2%。
表 4是本文方法的識別正確率與文獻[13]中CSP方法的比較。可以看出,本文提出的MVAR+MPCA方法的正確率在均值和標準差上都比CSP方法和EMD+CSP方法要好,b的正確率高出兩種CSP方法10%以上,f的正確率高出兩種CSP方法20%以上,標準差卻均小于兩種CSP方法,說明本文方法表現出良好的穩定性。這說明采用MVAR模型系數作為特征,并且結合MPCA特征降維方法適合處理多通道EEG信號。
4.4 實驗討論
由于腦信號是多通道信號,用AR模型將會忽略各個通道間的相互作用。因此本文采用MVAR模型對MEG/EEG信號進行研究。根據MVAR模型提取的系數特征是高維的特點,選擇結合MPCA特征降維方法,取得了良好的分類效果。實驗中本文方法對MEG/EEG信號都表現出了良好的穩定性,說明這種建模方法是合適的。除此之外,我們還對PCA特征降維進行了實驗,識別率遠沒有MPCA方法好。這說明,根據系數矩陣的特點選擇特征降維方法尤為重要。另一個問題,我們忽略掉不同通道噪聲源的相關性,對實驗數據重新進行了特征提取和分類實驗,結果表明不考慮通道間激勵噪聲相互作用會導致分類正確率下降。
5 結論
在BCI系統中,特征提取方法的選擇對于腦信號的正確分類起到關鍵性作用。本文對多通道MEG/EEG信號建立MVAR模型,將模型系數作為特征,并進行MPCA降維,分別用BCI競賽Ⅳ的第三組數據和第一組數據進行檢驗。MEG信號實驗結果表明,S1、S2的平均正確率達到43.5%,與競賽優勝者相比,除了比第一名低3.4%之外,領先于競賽第二、三名,S2的正確率高達45.5%,超出第一名10.9%,對兩組對象都表現出了良好的穩定性。除此之外,本文方法比其它文獻中的MGKCSP以及MCSP方法識別效果要好。EEG信號實驗結果表明,b的正確率高出兩種CSP方法10%以上,f的正確率高出兩種CSP方法20%以上;標準差卻比兩種CSP方法要小,說明本文方法表現出良好的穩定性。這兩組實驗說明這種建模方法是合適的。與用AR模型單個通道來處理多通道信號,和用傳統主成分分析特征降維相比,我們提出的MVAR模型和MPCA結合的特征提取方法對于處理多通道腦信號具有較高價值。下一步研究噪聲中的腦信號MVAR建模方法,以及多線性判別分析降維方法。
引言
腦機接口(brain-computer interface,BCI)依賴人的意識通過腦信號來對計算機或其他的外部設備進行控制[1]。如何提高腦電圖(electroencephalograph, EEG)和腦磁圖(magnetoencephalography, MEG)信號的識別性能仍是BCI研究中的關鍵問題[1]。目前腦信號的特征提取方法主要包括:小波包分解、自回歸(autoregression,AR)模型參數估計、時頻分析、相關性分析、共空間模式(common spatial patterns,CSP)等[2],其中AR模型在腦信號研究中應用廣泛。Lawhern等[3]采用AR模型對含有不同偽跡的連續EEG進行特征提取和分類。Keirn等[4]對每個通道EEG信號建立AR模型,將6個通道的AR模型系數連接起來作為特征進行分類。一般AR模型只適用于單通道信號,處理多通道EEG信號時存在局限性,例如忽略各個通道間相互作用。因此針對多通道信號建立的多變量自回歸(multivariate autoregressive,MVAR)模型更適合用于腦信號的研究[5]。薛建中等[6]給出了MVAR模型和核主成分分析降維方法結合方法并用于EEG信號識別。王江等[7]研究了MUAR模型算法并用于EEG信號特征提取。Zhao等[8]研究將EEG信號MVAR模型用于駕駛精神疲勞狀態的檢測。王寧等[9]研究了EEG信號MVAR模型用于情緒認知。除此之外MVAR模型在心電、肌電等信號的特征提取和分類等方面都有應用。Anderson等[10]對兩個意識任務、6個通道EEG信號進行了單變量和多變量AR模型特征提取的對比研究,結果表明MVAR模型系數作為特征能夠獲得更好的識別率。但是多通道腦信號通過建立MVAR模型求得的系數是矩陣,轉化為向量特征時會產生高維小樣本問題。
本文對多通道MEG/EEG信號建立MVAR模型,采用文獻[11]的歸一化LWR算法估計的MVAR模型系數矩陣作為特征。為了考慮系數矩陣的關聯性,提出采用多線性主成分分析(multilinear principal component analysis,MPCA)[12]對系數矩陣直接進行降維,而無需轉化為向量特征進行降維。最后分類器采用線性判別分析。新方法在BCI競賽Ⅳ的數據集3和1的實驗結果說明利用多通道信號處理方法提取MEG/EEG信號特征是可行的。
1 MVAR算法
由于腦信號是典型的多通道信號,因此首先建立腦信號的MVAR模型,然后給出求解MVAR系數矩陣的方法。
1.1 MVAR模型介紹
模型階數為m的d變量AR模型可以表示為
| $ \boldsymbol{X}(n)=\sum\limits_{i=1}^{m}{\boldsymbol{A} \left(i \right)}X\left(n-i \right)+\boldsymbol{E} \left(n \right) $ |
其中X(n)=(xi(n), …, xd(n))T是(d×1)的列向量,E(n)是(d×1)的激勵噪聲向量,n=0, …, N-1表示時間采樣點數,模型參數A(i)(i=1, 2, …, m)是(d×d)的預測系數矩陣,元素auv(i),u, v=1, …, d表示xv(n-i)對xu(i)的線性關聯作用,并且當u≠v時,auv≠avu。
1.2 MVAR模型系數矩陣求解
定義前、后向預測均方誤差分別為RmF=A m(i)R(-i)、R mG=Bm(i)R(i),A m(i)、B m(i)分別是m階前、后向預測第i個系數矩陣,前、后向預測均方誤差Δm=Am-1(i)R(m-i),其中自相關函數R(k)=E{ X(n)X(n-k)T}由樣本{X(0), X(2),…,X(N-1)}估計,即。
基于歸一化LWR算法求解M階MVAR模型系數的具體過程如下:
輸入:X(n), n=0, …, N-1,并設置R0G=P0=Q0=R0=R(0)=X(n)X(n)T,?0(0)= 0(0)=(R0G)-1/2, m=1
輸出:MVAR模型系數矩陣A
(1)計算前、后向均方誤差:m=?m-1(0)R(m)+?m-1(1)R(m-1)+…+? m-1(m-1)R(1)
(2)計算反射系數等中間變量值:ρm=m(Rm-1G)-T/2,Pm=Ⅰ-ρmρmT,Qm=Ⅰ-ρmTρm,(RmG)-1/2(Rm-1G)-1/2
(3)計算模型系數,其中k的取值從0~m
| $ \begin{align} & {{{\tilde{A}}}_{m}}\left(k \right)=P_{m}^{-1/2}\left[{{{\tilde{A}}}_{m-1}}\left(k \right)-{{\rho }_{m}}{{{\tilde{B}}}_{m-1}}\left(k \right)\right] \\ & {{{\tilde{B}}}_{m}}\left(k \right)=Q_{m}^{-1/2}\left[{{{\tilde{B}}}_{m-1}}\left(k \right)-\rho _{^{m}}^{T}{{{\tilde{A}}}_{m-1}}\left(k \right)\right] \\ \end{align} $ |
(4)當m<M時,令m=m+1,返回步驟(1)執行;當m=M時,輸出系數A(k)。
1.3 噪聲協方差矩陣的討論
預測均方誤差矩陣即模型中的噪聲源協方差矩陣,如果通道間激勵噪聲源相互獨立,則預測均方誤差是對角矩陣。然而實際中不同通道間的激勵噪聲源是相關的,所以其預測誤差是非對角矩陣。噪聲源的相關性對預測變量的影響可以通過模型系數的變化來體現,使得估計的系數更準確表示預測信號。這一思想可以通過以下變換來實現RMF=b Rdlag b *,其中b是通過對噪聲協方差矩陣進行Cholesky分解得到的下三角矩陣。因此MVAR模型的系數可以重新表示為Anew(k)=b -1A(k),k=0, …,m。
2 MPCA特征降維
對d通道信號建立m階MVAR模型,模型系數的數目為(d×d×m)。假設通道數為10,階數為6,則總數目共有600個,所以有必要進行特征降維處理以消除大量冗余特征。多通道腦信號通過建立MVAR模型求得的系數是矩陣形式,為了考慮系數矩陣的關聯性,提出采用MPCA方法對系數矩陣直接進行降維。
MPCA定義為張量空間RI1?RI2…?RIN'到張量子空間RP1?RP2…?RIN'的多線性變換[12],要求子空間維數Pn′小于原空間維數In′,當Pn′=In′時為全投影。投影公式為
| $ {{y}_{{{m}^{'}}}}={{x}_{{{m}^{'}}}}{{\text{ }\!\!\times\!\!\text{ }}_{1}}{{\widetilde{\boldsymbol{\text{U}}}}^{\left( 1 \right)T}}{{\text{ }\!\!\times\!\!\text{ }}_{2}}{{\widetilde{\boldsymbol{\text{U}}}}^{\left( 1 \right)T}}\cdots {{\text{ }\!\!\times\!\!\text{ }}_{N'}}{{\widetilde{\boldsymbol{\text{U}}}}^{\left( {{N}^{'}} \right)T}},{{m}^{'}}=1,\cdots ,{{M}^{'}},\ \ \ \ \sum\limits_{{{i}_{n'}}=1}^{{{p}_{n'}}}{\lambda _{{{i}_{n}}}^{\left( {{n}^{'}} \right)*}}/\sum\limits_{{{i}_{n'}}=1}^{{{I}_{n'}}}{\lambda _{{{i}_{{{n}^{'}}}}}^{\left( n \right)*}} $ |
其中M′為張量樣本的個數,N′為張量階數,滿足N′≥1。比率Q(n′)=表示n′階張量投影后保留的特征比例,λ(n′)*in′是第in′個全投影矩陣的n′階特征值。
是MPCA算法的目標函數最優化的解,即{∈RIN'×Pn′, n′=1, …, N′}為投影矩陣。
3 MVAR和MPCA結合的特征提取和分類方法
MVAR模型和MPCA結合的腦信號多通道特征提取方法簡要敘述如下:首先將多通道腦信號建立MVAR模型,用歸一化LWR算法求解模型系數。然后將訓練數據模型系數矩陣作零均值處理,求出對應的全投影矩陣,對其進行矩陣特征分解,確定子空間維數后,結合得到的特征向量和比率Q(n′),求得投影矩陣。最后將訓練和測試數據的模型系數矩陣投影到矩陣上,達到降維目的。
MVAR和MPCA結合的腦信號特征提取和分類過程如圖 1所示。圖中trail1、trail2分別表示受試者進行訓練實驗和測試實驗的次數,每次實驗采集腦信號的數據格式為N×d,N為采樣點數,d為通道數,m為MVAR模型的階數,圖中假設d=3,m=2。
 圖1
MVAR和MPCA結合的腦信號特征提取和分類示意圖
Figure1.
Diagram of brain signal feature extraction and classification based on MVAR combined with MPCA
圖1
MVAR和MPCA結合的腦信號特征提取和分類示意圖
Figure1.
Diagram of brain signal feature extraction and classification based on MVAR combined with MPCA
整個腦信號特征提取和分類實驗過程如下:
(1)分別對單次trail的訓練數據和測試數據(數據格式為N×d)建立m階MVAR模型,最后得到數據格式為trail×d×(d×m)的系數特征張量,可以看做是3階張量。
(2)訓練數據的系數特征張量經過MPCA特征降維,得到訓練特征,并且得到投影矩陣。
(3)測試數據得到的系數特征張量在投影矩陣上投影,得到測試特征。
(4)將降維后的訓練特征改寫成向量形式,訓練線性判別分析分類器。
(5)將測試特征改寫成向量形式,送進分類器得到分類結果。
4 實驗分析
文中采用BCI CompetitionⅣ:data sets 3和data sets 1數據,實驗數據來自http://www.bbci.de/competition/。
4.1 數據介紹
實驗數據一:BCI CompetitionⅣ:data sets 3包含兩個受試者S1和S2的10通道400個采樣點的前、后、左、右4類MEG信號,數據格式表示為:實驗次數×時間采樣點數×通道數。因此,S1和S2的訓練數據分別為160×400×10和160×400×10,測試數據分別為74×400×10和73×400×10。
實驗數據二:BCI CompetitionⅣ:data sets 1包含多個健康受試者運動想象任務的59通道100個采樣點的2類EEG信號。本文實驗選擇與參考文獻[13]相同的11個通道EEG信號進行實驗,并選擇b和f受試者數據進行實驗,b和f受試者的訓練集數據格式為140×100×11,測試集數據格式為60×100×11。
4.2 實驗參數介紹
Q表示投影后在子空間中保存原始維數的比例,實驗中選擇95%~100%。
m表示MVAR模型的階數,實驗一階數選取3~7階,實驗二階數選取2~6階。
4.3 實驗結果分析
4.3.1 實驗數據一的結果
表 1為S1、S2在不同實驗參數下的識別正確率。可以看出,S1最高識別正確率為41.89%,此時MVAR模型階數為3,Q為98%。S2最高識別正確率為45.21%,此時MVAR模型階數為6,Q為100%。由實驗結果可知,MVAR系數矩陣進行MPCA降維能夠得到較好實驗結果。
表 2為本文方法與競賽前三名以及文獻[14]中多類別廣義核CSP(MGKCSP)方法和多類CSP(MCSP)方法測試集識別正確率的比較。可以知道,我們采用的MVAR模型系數作為特征并進行MPCA特征降維的方法,平均值超過MGKCSP方法12%,超過MCSP方法1.4%,超過第二名將近18%,超過第三名將近20%,具有絕對性的優勢。第二名和第三名都是采用時域或頻域特征,而MVAR方法也是采用時域或頻域特征,但效果明顯更好。MGKCSP方法和MCSP方法采用空域特征,MVAR方法優于MGKCSP方法,與MCSP方法相當。與第一名相比,雖然S1的正確率不高,但是平均值差僅差約3.4%。而S2的正確率為45.2%,超出第一名10.9%,超出MCSP方法9.6%。對于S2測試數據識別正確率的實驗,相關文獻的實驗結果都不好,而本文卻得出45.2%的優異結果。這說明采用MVAR模型系數作為特征,并且結合MPCA特征降維方法對于S1和S2分類具有很好的穩定性,新方法適合處理多通道MEG信號,應該很有推廣的價值。
4.3.2 實驗數據二的結果
表 3為b、f在不同實驗參數下的識別正確率,表示10次測試集分類正確率的均值和標準差。可以看出,MVAR模型的階數為2,Q為100%時,b的最高識別正確率均值為69.3%,標準差為3.6%;f的最高識別正確率均值為82.8%,標準差為3.2%。
表 4是本文方法的識別正確率與文獻[13]中CSP方法的比較。可以看出,本文提出的MVAR+MPCA方法的正確率在均值和標準差上都比CSP方法和EMD+CSP方法要好,b的正確率高出兩種CSP方法10%以上,f的正確率高出兩種CSP方法20%以上,標準差卻均小于兩種CSP方法,說明本文方法表現出良好的穩定性。這說明采用MVAR模型系數作為特征,并且結合MPCA特征降維方法適合處理多通道EEG信號。
4.4 實驗討論
由于腦信號是多通道信號,用AR模型將會忽略各個通道間的相互作用。因此本文采用MVAR模型對MEG/EEG信號進行研究。根據MVAR模型提取的系數特征是高維的特點,選擇結合MPCA特征降維方法,取得了良好的分類效果。實驗中本文方法對MEG/EEG信號都表現出了良好的穩定性,說明這種建模方法是合適的。除此之外,我們還對PCA特征降維進行了實驗,識別率遠沒有MPCA方法好。這說明,根據系數矩陣的特點選擇特征降維方法尤為重要。另一個問題,我們忽略掉不同通道噪聲源的相關性,對實驗數據重新進行了特征提取和分類實驗,結果表明不考慮通道間激勵噪聲相互作用會導致分類正確率下降。
5 結論
在BCI系統中,特征提取方法的選擇對于腦信號的正確分類起到關鍵性作用。本文對多通道MEG/EEG信號建立MVAR模型,將模型系數作為特征,并進行MPCA降維,分別用BCI競賽Ⅳ的第三組數據和第一組數據進行檢驗。MEG信號實驗結果表明,S1、S2的平均正確率達到43.5%,與競賽優勝者相比,除了比第一名低3.4%之外,領先于競賽第二、三名,S2的正確率高達45.5%,超出第一名10.9%,對兩組對象都表現出了良好的穩定性。除此之外,本文方法比其它文獻中的MGKCSP以及MCSP方法識別效果要好。EEG信號實驗結果表明,b的正確率高出兩種CSP方法10%以上,f的正確率高出兩種CSP方法20%以上;標準差卻比兩種CSP方法要小,說明本文方法表現出良好的穩定性。這兩組實驗說明這種建模方法是合適的。與用AR模型單個通道來處理多通道信號,和用傳統主成分分析特征降維相比,我們提出的MVAR模型和MPCA結合的特征提取方法對于處理多通道腦信號具有較高價值。下一步研究噪聲中的腦信號MVAR建模方法,以及多線性判別分析降維方法。