傳統樣本熵很難量化信號本身固有的遠程相關性, 雖然多尺度熵能夠檢測數據內在相關性, 但其多用于單變量信號。多元多尺度熵作為多尺度熵在多元信號上的推廣, 是非線性動態相關性的一種反映, 但是傳統的多元多尺度熵計算量大, 對于通道數較多的系統需要耗費大量的時間和空間, 并且無法準確地反映變量間的相關性。本文提出的改進的多元多尺度熵, 將傳統的多元多尺度熵針對單個變量的嵌入模式改為對所有變量同時嵌入, 不但解決了隨著通道數增加內存溢出的問題, 也更適用于實際多變量信號分析。本文方法對仿真數據及波恩癲癇數據進行了試驗, 仿真結果表明該方法對相關性數據具有良好的區分性能; 癲癇數據實驗表明, 該方法對5個數據集均具有較好的分類精度, 其中對數據集Z、S的分類精度達100%。
引用本文： 徐永紅, 崔潔, 洪文學, 梁會娟. 基于改進多元多尺度熵的癲癇腦電信號自動分類. 生物醫學工程學雜志, 2015, 32(2): 256-262. doi: 10.7507/1001-5515.20150047 復制
引言
癲癇是一種常見的慢性腦部疾病，其在臨床上呈現的突發性和強破壞性是癲癇患者致殘和死亡的重要原因。因此，對癲癇進行自動分析，以便及時采取相應的措施就具有重要的臨床意義。
近似熵[1]描述了系統的非線性動力學特性，它在理論上反映了信號的不規則性及復雜程度。相對于K-S熵、K2熵、E-R熵而言，近似熵使用較短的數據就可以獲取比較穩健的信號特征。針對近似熵對微小的復雜性變化不敏感的缺點，Richman等[2-3]提出將樣本熵作為復雜性測度方法，并將其廣泛應用于生理時間序列分析中。隨著非線性動力學的發展，復雜性分析已經成為研究腦電(electroencephalogram, EEG)時間序列的流行趨勢，它能夠反映系統的動態特性。近年來研究者將熵用于分析癲癇EEG時間序列，并在該領域逐漸流行[4]。文獻[5]分別用近似熵和樣本熵對癲癇患者的EEG信號進行分析比較，樣本熵的變化幅度明顯大于近似熵，其變化幅度相對于近似熵提高了10％~25％。文獻[6]提出了一種基于極端學習機和近似熵的EEG信號檢測方法。首先，計算EEG信號的近似熵作為非線性特征，并與小波變換提取的波動指數結合，組成特征向量，然后將特征向量送入單隱層前饋神經網絡，采用ELM學習算法訓練網絡，從而提高分類精度。文獻[7]將排序熵用于分析人類EEG，證明人類癲癇發作時的排序熵值大于正常時的熵值，為癲癇EEG信號的檢測提供了依據。文獻[8]首先利用小波包熵特征提取的方法分析癲癇EEG信號，對癲癇EEG進行不同層數的小波包分解，將每層小波的近似熵作為特征對其進行檢測。文獻[9]中多尺度樣本熵揭示了時間序列的長期相關性及生物信號的復雜性。但是大多數生理信號為多元信號，因而文獻[10]對多尺度熵進行了擴展，首次提出了多元多尺度熵，將其應用于心電和呼吸信號，有效地揭示了普通樣本熵無法描述的生物信號的遠程相關性，而這種遠程相關性是實際復雜系統的重要特征。
本文在文獻[11]提出的傳統的多元多尺度熵的基礎上進行了改進，并將其用于癲癇EEG信號分析。首先對原始單通道EEG信號進行小波包分解，選取癲癇EEG信號對應頻帶，也就是將一元信號轉化為多元信號；然后利用改進的多元多尺度熵提取多尺度特征；最后利用不同分類器進行分類并對分類結果進行比較。
1 本文算法
1.1 傳統的多元多尺度熵算法[11 ]
傳統的多元多尺度熵包含兩部分：
(1) 定義t個變量的時間序列{xk, i}i=1N，k=1, 2, …, t的粗粒化過程，尺度因子隨著粗粒化長度的增加而增加，N代表每個變量的采樣點數。對于某一尺度ω，粗粒化后的多元時間序列為
| $y_{k, j}^\omega=\frac{1}{\omega }\sum\limits_{i=\left({j-1} \right)\omega + 1}^{j\omega } {{x_{k, i}}}, $ |
其中，變量數k=1, 2, …, t。
(2) 對于每個粗粒化多元時間序列yk, jω，估計其多元樣本熵(multivariate sample entropy, MSE)。
在計算多元多尺度熵的過程中，MSE的估計是很重要的因素。下面介紹傳統MSE理論，并由此得到傳統多元多尺度熵。
若要計算MSE，首先要了解多元嵌入理論[12]。t個變量的時間序列{xk, j}i=1N，k=1, 2, …, t基于復合延遲向量進行多元嵌入重構
| ${X_m}\left(i \right)=\left[\begin{array}{l} {x_{1, i}}, {x_{1, i + {\lambda _1}}}, \cdots, {x_{1, i + \left({{m_1}-} \right){\lambda _1}}}, {x_{2, i, }}{x_{2, i + {\lambda _2}}}, \ \cdots, {x_{2, i + \left({{m_2}-1} \right){\lambda _2}}}, \cdots, {x_{t, i}}, {x_{t, i + {\lambda _1}}}, \cdots, {x_{t, \left({{m_t}-1} \right){\lambda _t}}} \end{array} \right], $ |
其中嵌入向量為Mm(i)=[m1, m2, …, mt]∈Rt，時間延遲向量為λ=[λ, λ, …, λt]，復合延遲向量Xm(i)∈Rm, m=k=1tmk。
傳統多元樣本熵計算步驟：
(1) 定義復合延遲向量Xm(i)∈Rm, i=1, 2, …, N-n，其中n=max{M}×max{λ}
(2) 定義兩個復合延時向量的距離
| $\begin{array}{c} d\left[{{X_m}\left(i \right), {X_m}\left(j \right)} \right]={\max _{l=1, 2, \cdots, m}}\left\{ {\left| {x\left({i + l-1} \right)} \right.} \right.\ \left. {\left. {x\left({j + l-1} \right)} \right|} \right\} \end{array}$ |
(3) 對于給定的復合延時向量Xm(i)及閾值r，計算滿足上述條件的距離Di的個數
| $d\left[{{X_m}\left(i \right), {X_m}\left(j \right)} \right] \le r, j \ne i, $ |
計算其出現頻率，，得到嵌入向量Mm(i)時的條件概率
| ${P^m}\left(r \right)=\frac{1}{{N-n}}\sum\limits_{i=1}^{N-n} {P_i^m\left(r \right)} $ |
(4) 擴展多元延遲向量的維數從m維至m+1維。有t種不同的方式將嵌入向量Mm(i)=[m1, m2, …, mt]擴展到Mm(i)=[m1, m2, …mk+1, …, mt](k=1, 2, …, t)。因此，在空間Rm+1中可以就可以得到t×(N-n)個向量Xm+1(i)，Xm+1(i)表示對于變量k，嵌入維度從mk增加到mk+1時的復合延遲向量。在嵌入過程中，其他數據通道的嵌入維度不變，也就是系統的總嵌入維度從m增加到m+1。
(5) 對于給定的Xm+1(i)，當d[Xm+1(i), Xm+1(j)]≤r, j≠i時，計算向量Si的數量。統計其出現頻率，，得到嵌入向量Mm+1(i)時的條件概率
| $P_i^{m + 1}\left(r \right)=\frac{1}{{t\left({N-n} \right)}}\sum\limits_{i=1}^{t\left({N-n} \right)} {P_i^{m + 1}\left(r \right)} $ |
(6) Pm(r)和Pm+1(r)分別表示嵌入維度為m、m+1時，兩個復合延遲向量相似性的條件概率。對于相似容限r，多元樣本熵表示嵌入維度m、m+1時兩個條件概率的比值的負自然對數
| $MSE\left({M, \lambda, r, N} \right)=-\ln \left[{\frac{{{P^{m + 1}}\left(r \right)}}{{{P^m}\left(r \right)}}} \right]$ |
1.2 改進的多元多尺度熵
改進的多元多尺度熵與傳統多元多尺度熵計算步驟相似，首先對時間序列{xk, i}i=1N, k=1, 2, …, t進行粗粒化，對于尺度ω，粗粒化后的多元時間序列
| $y_{k, j}^\omega=\frac{1}{\omega }\sum\limits_{i=\left({j-1} \right)\omega + 1}^{j\omega } {{x_{k, i}}, } $ |
其次，計算改進多元樣本熵。本文主要是對多元樣本熵的計算過程進行了改進。
改進多元樣本熵(improved multivariate sample entropy，IMSE)的計算步驟：
(1) 定義復合延遲向量Xm(i)∈Rm, i=1, 2, …, N-n，其中n=max {M}×max{λ}
(2) 定義Xm(i)與Xm(j)的距離d[Xm(i), Xm(j)]為兩者對應元素中差值最大的一個:
| $\begin{array}{c} d\left[{{X_m}\left(i \right), {X_m}\left(j \right)} \right]={\max _{n=1, 2, \cdots, m}}\left\{ {\left| {x\left({i + l-1} \right)} \right.-} \right.\ \left. {\left. {x\left({j + l-1} \right)} \right|} \right\} \end{array}$ |
(3) 對于給定的閾值r(r＞0)，對每個i值統計d[Xm(i), Xm(j)]≤r, j≠i的數目與總個數N-n-1的比值，記為，再求所有i的平均值
| ${P^m}\left(r \right)=\frac{1}{{N-n}}\sum\limits_{i=1}^{N-n} {P_i^m\left(r \right)} $ |
(4) 擴展多元延遲向量的維數從m維至m+1維。嵌入維度為m+1時，嵌入向量擴展為：
| ${M_{m + 1}}\left(i \right)=\left[{{{\left({m + 1} \right)}_1}, {{\left({m + 1} \right)}_2}, \cdots, {{\left({m + 1} \right)}_t}} \right]$ |
因此，在空間Rm+1中就可以得到N-n個復合延遲向量Xm+1(i)，Xm+1(i)表示嵌入維度從mk增加到mk+1時的復合延遲向量。
(5) 嵌入維度m+1，重復步驟(1)~(3)，得到
| ${P^{m + 1}}\left(r \right)=\frac{1}{{N-n}}\sum\limits_{i=1}^{N-n} {P_i^{m + 1}\left(r \right), } $ |
式中Pim+1(r)表示在時間尺度λ上，以X(i)為中心，在嵌入維度m+1情形下，向量mm(i)與Xm(i)的距離d[Xm(i), Xm(j)]小于等于r的概率，表示所有Xm(i)與Xm(j)的關聯程度，也就是表示序列{xk, i}i=1N的規律性程度。而均值Pm+1(r)則表示在尺度λ下的時間序列的自相關程度。
(6) 計算IMSE
| $IMSE\left({M, \lambda, r, N} \right)=-\ln \left[{\frac{{{P^{m + 1}}\left(r \right)}}{{{P^m}\left(r \right)}}} \right]$ |
傳統多元多尺度熵計算MSE時，嵌入維度為m+1，則嵌入向量中只有一組向量嵌入為m+1，其他保持不變，即Mm(i)=[m1, m2, …, mk+1, …, mt](k=1, 2, …, t)，對于每個變量嵌入N-n次，得到N-n個復合延遲向量Xm(i)。t個變量的時間序列嵌入后復合延遲向量數為t(N-n)。即多元嵌入復合延遲向量為各變量依次嵌入的累積，則距離d[Xm(i), Xm(j)]的計算出現冗余重復。
而本文提出的改進方法在嵌入維度為m+1時，嵌入向量中所有向量均嵌入為m+1，也就是Mm+1(i)=[(m+1)1, (m+1)2, …, (m+1)t]，相對于傳統方法，本文方法不再針對每一個變量，而是針對所有變量，對于t個變量，總的復合延遲向量Xm(i)數為N-n，計算任意兩個向量間的距離，比傳統t(N-n)個復合延遲向量兩兩計算距離減小了計算量，因而計算速度更快。由于實際生理信號大多通道數較多，傳統方法在信號采樣點數為1 000、通道大于10時計算量大，復雜度高，使計算機內存溢出，無法有效計算；而本文提出方法則更具有普遍適用性，即使通道數較多(如64)也能有效地計算，因而本文提出方法更能滿足實際多元時間序列的需要。
2 實驗分析
2.1 仿真分析
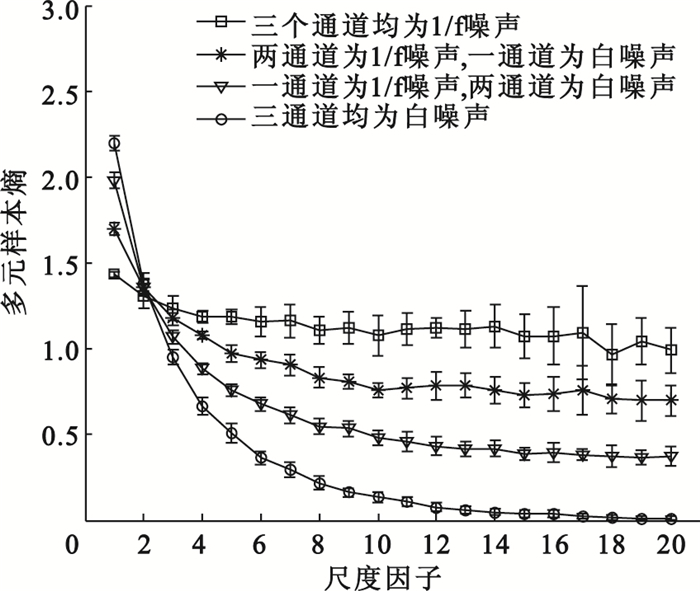
文獻[13]中分析了單通道時多尺度熵的特點，對于不相關的隨機白噪聲信號，其樣本熵隨著尺度的增加單調遞減；而對于具有遠程相關性的1/f噪聲信號，信號的樣本熵隨尺度的變化無明顯改變。這就說明了對于單通道信號1/f噪聲比不相關的隨機白噪聲更加復雜。為了闡明改進的多元多尺度熵具有同樣的特性，實驗分析了不相關的隨機白噪聲和1/f噪聲生成的4個3通道的時間序列信號。對于每個時間序列在計算改進的多元多尺度熵時所用參數都相同，M=2、tau=1、r=0.3×std(std表示歸一化時間序列的標準偏差)，圖 1為對應的3通道信號多元多尺度熵的變化曲線。如圖所示，隨著1/f噪聲的增加，MSE在較高尺度上逐漸增大。當3個通道都是1/f噪聲時，復雜度在高尺度上達到最大。因而采用多元多尺度熵驗證區分隨機白噪聲和1/f噪聲是十分有效且方便的。同時也可得出以下結論：在具有遠程相關的多元時間序列中，遠程相關的變量越多，系統的復雜度越高。
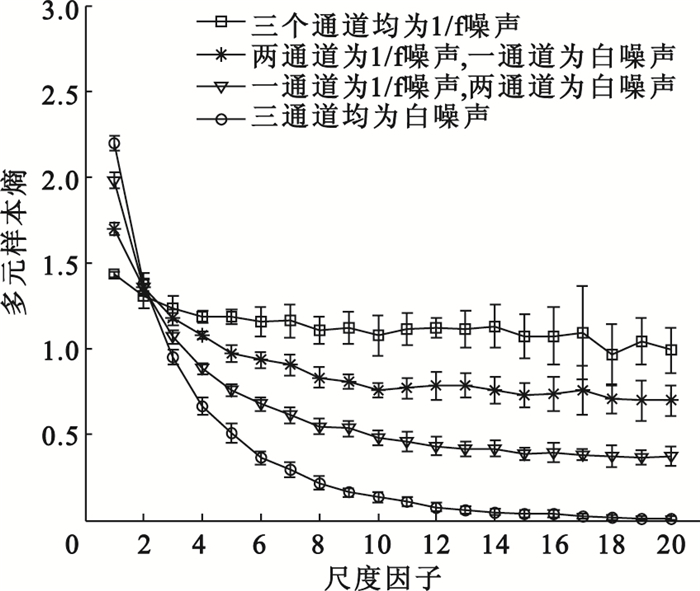圖1
三通道(白噪聲、1/f噪聲)改進的多元多尺度熵分析
Figure1.
Improved multivariate multiscale entropy analysis of three channels (white noise and 1/f noise)
一般的多尺度熵只反映了單通道信號的遠程相關性，對于多通道數據，數據間的相關性及交互信息就無法有效地描述。而本文提出的改進多元多尺度熵對多元數據通道內及通道間的相關性都能進行有效的描述。
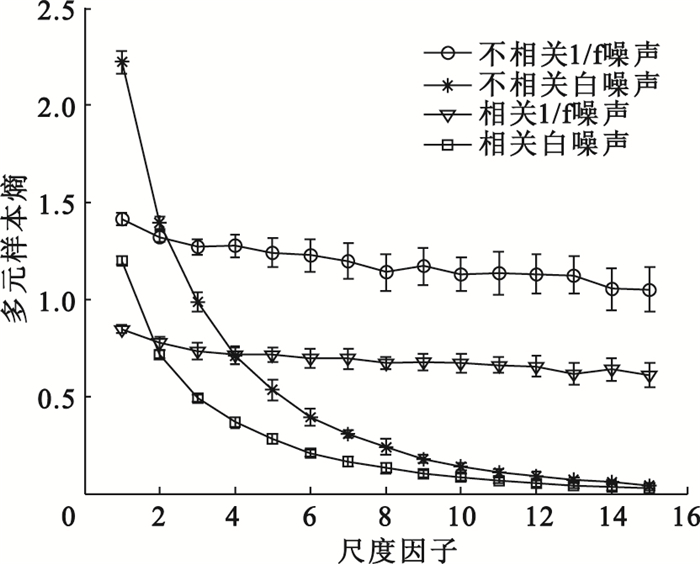
為了充分體現改進的多元多尺度熵的優越性，分別生成3通道相關1/f噪聲與不相關1/f噪聲，相關隨機白噪聲與不相關隨機白噪聲信號。文獻[14]表明傳統的多尺度方法只反映了通道內的相關性，對于多通道間相關與不相關的白噪聲與1/f噪聲不能進行有效區分。如圖 2所示，本文提出的改進的多元多尺度熵既反映了通道內的遠程相關性，又反映了通道間的相關性。對于相關與不相關的無論是白噪聲還是1/f噪聲，在某些尺度都具有良好的區分度。不相關的1/f噪聲在較高的尺度上復雜度最高，而相關白噪聲最低。由相關數據的物理意義可知，數據間的相關度越高則復雜度越小，其相應熵值也就越小；數據間的相關度越低則復雜度越大，其相應熵值也就越大。采用本文方法，不相關的1/f噪聲和白噪聲在各尺度熵值均大于相關的1/f噪聲和白噪聲，具有明確的物理意義。
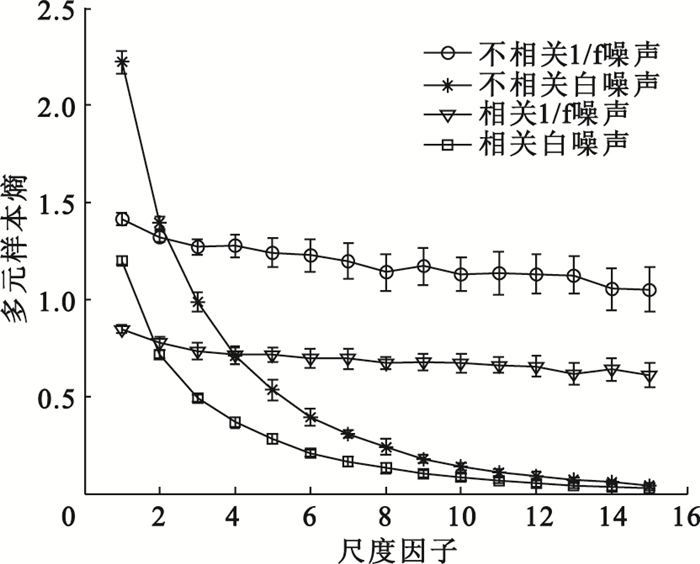圖2
改進的多元多尺度熵相關性分析比較
Figure2.
Correlation analysis comparison of improved multivariate multiscale entropy
2.2 癲癇數據實驗分析
本文數據來源于德國波恩癲癇研究室的癲癇數據庫，數據庫中含有5個數據集，依次用Z、O、N、F、S的5個字母表示，每個集合包含100個單通道EEG數據段，長度均為23.6 s。數據集Z記錄了志愿者清醒睜眼狀態的EEG，O記錄了清醒閉眼狀態的EEG，N記錄了致癇灶對側域，F記錄了致癇灶內域，都是在沒有癲癇發作時的EEG記錄，只有S記錄了致癇灶內域癲癇活動。本文針對5個數據集進行研究，其中數據集中的前50段為訓練樣本，后50段為測試樣本。
為了能有效地識別癲癇EEG信號特點，首先對癲癇EEG信號進行小波包分解。在分解的過程中，節點的選取既要覆蓋癲癇腦電波的特征頻帶，又要最大限度地節約時間和空間。因此對原始信號選取DB4小波基，進行3層小波分解。
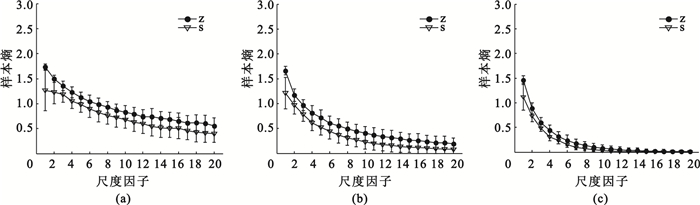
為了將改進的多元多尺度熵與傳統的多元多尺度熵進行更好的比較，首先選取數據集Z、S進行分析。對兩種方法選取同樣的參數：M=2、tau=1、r=0.3×std (std歸一化癲癇EEG信號的標準偏差)。如圖 3所示，對原始癲癇數據進行3層小波包分解，選取同樣的頻帶范圍，對于單個頻帶計算其多尺度樣本熵，在3個頻帶范圍內兩個數據集的多尺度樣本熵均值方差曲線距離近，且在大多尺度上有明顯的交叉重疊，因而在各頻帶多尺度樣本熵不能有效地區分數據集Z、S。
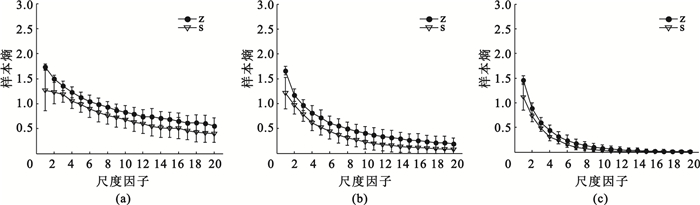圖3
單頻帶多尺度樣本熵
(a)0~10.85 Hz多尺度樣本熵；(b)10.85~21.7 Hz多尺度樣本熵；(c)21.7~32.55 Hz多尺度樣本熵
Figure3. Single band multiscale entropy of samples(a) 0-10.85 Hz multiscale samples entropy; (b) 10.85-21.7 Hz multiscale samples entropy; (c) 21.7-32.55 Hz multiscale samples entropy
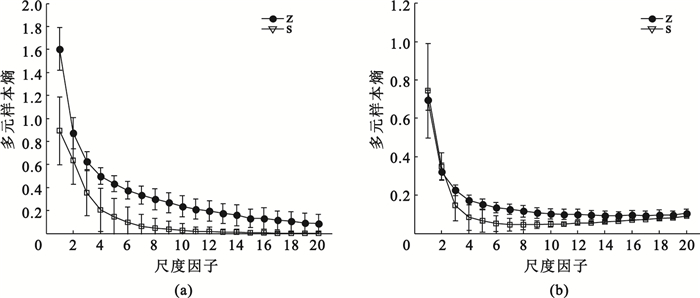
對于多元信號，傳統的樣本熵無法對其進行描述，然而改進的多元多尺度熵可體現出明顯的優越性。圖 4(a)為數據集Z、S的100個樣本改進的多元多尺度熵均值方差曲線；圖 4(b)為傳統的多元多尺度熵的均值方差曲線。改進的多元多尺度熵兩個數據集的均值在各尺度上相距較遠，方差曲線在大
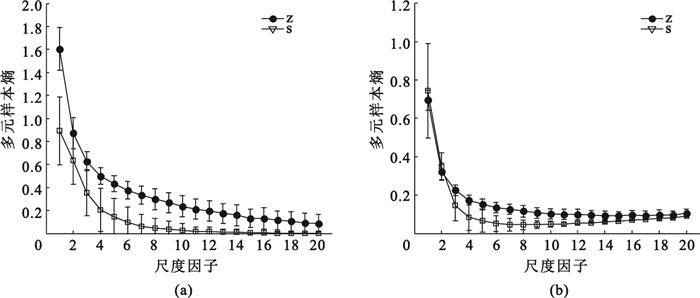圖4
三個頻帶時傳統的多元多尺度熵與改進的多元多尺度熵結果比較
(a)數據集Z、S三頻帶改進的多元多尺度熵；(b)數據集Z、S三頻帶傳統的多元多尺度熵
Figure4. Comparison of three frequent bands results between traditional multivariate multiscale entropy and improved multivariate multiscale entropy(a) improved multivariate multiscale entropy of three frequent bands (dataset Z, S); (b) traditional multivariate multiscale entropy of three frequent bands (dataset Z, S)
多數尺度上無交叉重疊，因而具有良好的可分性；而傳統的多元多尺度熵均值曲線距離近，方差曲線在大多數尺度上重疊明顯，可分性差。雖然改進的方法對于一元信號沒有表現出明顯的優越性，但是對于多元信號而言，改進的方法明顯優于傳統方法。
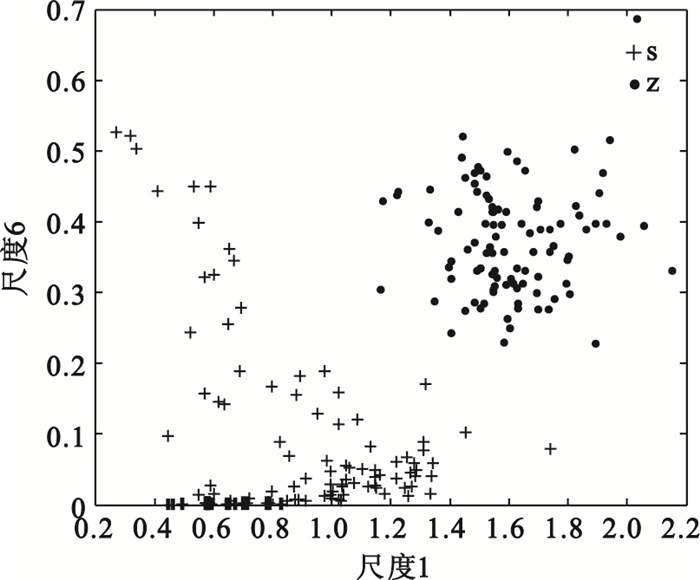
應用本文提出的改進的多元多尺度熵，僅選取尺度1和尺度6作為特征，如圖 5所示兩類的可區分性極其顯著，即使應用簡單的分類器也能獲得很高的分類精度。因而說明應用本文提出的特征提取方法，需要很少的特征就能獲得很高的分類精度。在改進的多元多尺度熵中，各尺度上的值表示在該尺度粗粒化時間序列的多元樣本熵，如圖的兩個特征分別表示尺度1、6上的改進多元樣本熵，描述了在相應尺度上的復雜度，也就是說改進多元多尺度熵的不同尺度特征均有其物理意義。
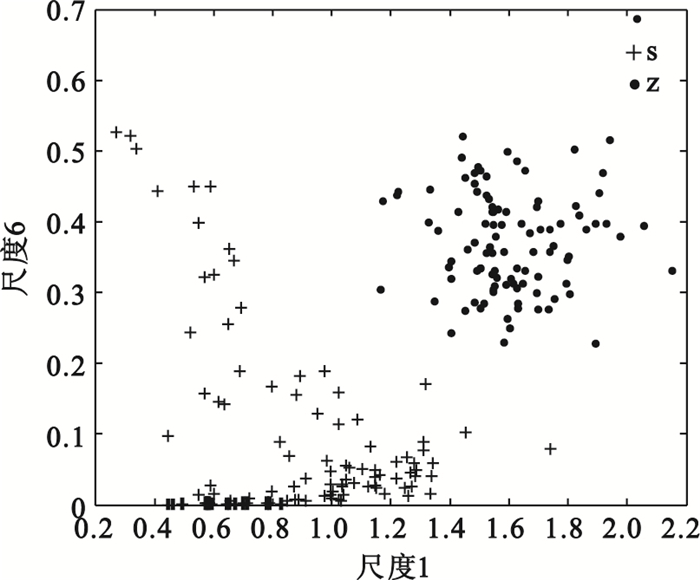圖5
數據集Z、S兩個尺度上改進的MSE
Figure5.
Improved MSE (Data sets Z, S) with two scales
本文提出的方法不僅在分類精度上有明顯提高，還大大提高了計算速度。為了將本文提出方法與傳統方法比較，對原始癲癇EEG信號利用小波包進行4層分解，獲取不同頻帶的數據信號，隨著通道數的增加，計算時間如表 1所示。從表 1可以看出，隨著數據長度的增加，兩種方法的計算時間都明顯增加，但是無論數據長度是多少，就多元信號而言，改進方法的計算時間都要比傳統方法短。
表1
傳統的多元多尺度熵與改進的多元多尺度熵運行時間比較
Table1.
Comparison of execution time between traditional multivariate multiscale entropy and improved multivariate multiscale entropy
最后，對不同數據集組合進行分類比較，對各數據集均選取區分度較好的尺度作為特征進行分類。本文中采用的分類器分別為概率神經網絡(probabilistic neural network, PNN)、支持向量機(support vector machine，SVM)、線性判別分類器(linear discrimination analysis，LDA)，送入到不同分類器的特征數據均相同，不同的數據集組合分類精度如表 2所示。
表2
不同分類器分類結果比較
Table2.
Comparison of classified results between different classifiers
由三種不同分類器在相同條件下的分類結果可以看出，對于本文提取出的特征, 應用相對簡單的分類器反而可以得到較高的分類精度，對各數據集最高正確率分別為100%、96.7%、90.3%。與目前國際上針對各數據集組合的特征提取與分類結果相比，本文所提出的方法體現出明顯的優越性，具體結果如表 3所示。
表3
不同特征提取及分類方法識別結果對比
Table3.
Recognition result comparison between different feature extractions and classifications
3 結論
本文提出的改進的多元多尺度熵，相對于單尺度熵能更好地反映通道內及通道間的相關性，還能夠提供更加豐富的多元觀測信號的動態特性，獲取比標準的多尺度熵更高的自由度。相對于傳統的多元多尺度熵，本文在嵌入維數為m+1時，對算法進行了改進。傳統方法對于變量k，嵌入向量擴展為Mm(i)=[m1, m2, …, mk+1…, mt](k=1, 2, …, t)，而改進方法對所有變量嵌入向量擴展為Mm(i)=[(m+1)1, (m+1)2, …, (m+1)t]。因此，在距離計算過程中，復合延時向量數為原來的1/t，解決了傳統的多元多尺度熵隨著通道數增加內存很快溢出的問題，因而更適用于實際工作中多通道的生理信號分析。
由于實際EEG信號高頻部分多為噪聲干擾，本文將小波包分解與改進的多元多尺度熵相結合，能很好地濾除干擾信號。以不同尺度上的改進的多元樣本熵作為特征，縮短了計算時間，獲得更好的癲癇EEG信號區分度。本文只將該方法用于癲癇EEG信號分析，如何應用于其他領域是下一步需要進行的工作。
引言
癲癇是一種常見的慢性腦部疾病，其在臨床上呈現的突發性和強破壞性是癲癇患者致殘和死亡的重要原因。因此，對癲癇進行自動分析，以便及時采取相應的措施就具有重要的臨床意義。
近似熵[1]描述了系統的非線性動力學特性，它在理論上反映了信號的不規則性及復雜程度。相對于K-S熵、K2熵、E-R熵而言，近似熵使用較短的數據就可以獲取比較穩健的信號特征。針對近似熵對微小的復雜性變化不敏感的缺點，Richman等[2-3]提出將樣本熵作為復雜性測度方法，并將其廣泛應用于生理時間序列分析中。隨著非線性動力學的發展，復雜性分析已經成為研究腦電(electroencephalogram, EEG)時間序列的流行趨勢，它能夠反映系統的動態特性。近年來研究者將熵用于分析癲癇EEG時間序列，并在該領域逐漸流行[4]。文獻[5]分別用近似熵和樣本熵對癲癇患者的EEG信號進行分析比較，樣本熵的變化幅度明顯大于近似熵，其變化幅度相對于近似熵提高了10％~25％。文獻[6]提出了一種基于極端學習機和近似熵的EEG信號檢測方法。首先，計算EEG信號的近似熵作為非線性特征，并與小波變換提取的波動指數結合，組成特征向量，然后將特征向量送入單隱層前饋神經網絡，采用ELM學習算法訓練網絡，從而提高分類精度。文獻[7]將排序熵用于分析人類EEG，證明人類癲癇發作時的排序熵值大于正常時的熵值，為癲癇EEG信號的檢測提供了依據。文獻[8]首先利用小波包熵特征提取的方法分析癲癇EEG信號，對癲癇EEG進行不同層數的小波包分解，將每層小波的近似熵作為特征對其進行檢測。文獻[9]中多尺度樣本熵揭示了時間序列的長期相關性及生物信號的復雜性。但是大多數生理信號為多元信號，因而文獻[10]對多尺度熵進行了擴展，首次提出了多元多尺度熵，將其應用于心電和呼吸信號，有效地揭示了普通樣本熵無法描述的生物信號的遠程相關性，而這種遠程相關性是實際復雜系統的重要特征。
本文在文獻[11]提出的傳統的多元多尺度熵的基礎上進行了改進，并將其用于癲癇EEG信號分析。首先對原始單通道EEG信號進行小波包分解，選取癲癇EEG信號對應頻帶，也就是將一元信號轉化為多元信號；然后利用改進的多元多尺度熵提取多尺度特征；最后利用不同分類器進行分類并對分類結果進行比較。
1 本文算法
1.1 傳統的多元多尺度熵算法[11 ]
傳統的多元多尺度熵包含兩部分：
(1) 定義t個變量的時間序列{xk, i}i=1N，k=1, 2, …, t的粗粒化過程，尺度因子隨著粗粒化長度的增加而增加，N代表每個變量的采樣點數。對于某一尺度ω，粗粒化后的多元時間序列為
| $y_{k, j}^\omega=\frac{1}{\omega }\sum\limits_{i=\left({j-1} \right)\omega + 1}^{j\omega } {{x_{k, i}}}, $ |
其中，變量數k=1, 2, …, t。
(2) 對于每個粗粒化多元時間序列yk, jω，估計其多元樣本熵(multivariate sample entropy, MSE)。
在計算多元多尺度熵的過程中，MSE的估計是很重要的因素。下面介紹傳統MSE理論，并由此得到傳統多元多尺度熵。
若要計算MSE，首先要了解多元嵌入理論[12]。t個變量的時間序列{xk, j}i=1N，k=1, 2, …, t基于復合延遲向量進行多元嵌入重構
| ${X_m}\left(i \right)=\left[\begin{array}{l} {x_{1, i}}, {x_{1, i + {\lambda _1}}}, \cdots, {x_{1, i + \left({{m_1}-} \right){\lambda _1}}}, {x_{2, i, }}{x_{2, i + {\lambda _2}}}, \ \cdots, {x_{2, i + \left({{m_2}-1} \right){\lambda _2}}}, \cdots, {x_{t, i}}, {x_{t, i + {\lambda _1}}}, \cdots, {x_{t, \left({{m_t}-1} \right){\lambda _t}}} \end{array} \right], $ |
其中嵌入向量為Mm(i)=[m1, m2, …, mt]∈Rt，時間延遲向量為λ=[λ, λ, …, λt]，復合延遲向量Xm(i)∈Rm, m=k=1tmk。
傳統多元樣本熵計算步驟：
(1) 定義復合延遲向量Xm(i)∈Rm, i=1, 2, …, N-n，其中n=max{M}×max{λ}
(2) 定義兩個復合延時向量的距離
| $\begin{array}{c} d\left[{{X_m}\left(i \right), {X_m}\left(j \right)} \right]={\max _{l=1, 2, \cdots, m}}\left\{ {\left| {x\left({i + l-1} \right)} \right.} \right.\ \left. {\left. {x\left({j + l-1} \right)} \right|} \right\} \end{array}$ |
(3) 對于給定的復合延時向量Xm(i)及閾值r，計算滿足上述條件的距離Di的個數
| $d\left[{{X_m}\left(i \right), {X_m}\left(j \right)} \right] \le r, j \ne i, $ |
計算其出現頻率，，得到嵌入向量Mm(i)時的條件概率
| ${P^m}\left(r \right)=\frac{1}{{N-n}}\sum\limits_{i=1}^{N-n} {P_i^m\left(r \right)} $ |
(4) 擴展多元延遲向量的維數從m維至m+1維。有t種不同的方式將嵌入向量Mm(i)=[m1, m2, …, mt]擴展到Mm(i)=[m1, m2, …mk+1, …, mt](k=1, 2, …, t)。因此，在空間Rm+1中可以就可以得到t×(N-n)個向量Xm+1(i)，Xm+1(i)表示對于變量k，嵌入維度從mk增加到mk+1時的復合延遲向量。在嵌入過程中，其他數據通道的嵌入維度不變，也就是系統的總嵌入維度從m增加到m+1。
(5) 對于給定的Xm+1(i)，當d[Xm+1(i), Xm+1(j)]≤r, j≠i時，計算向量Si的數量。統計其出現頻率，，得到嵌入向量Mm+1(i)時的條件概率
| $P_i^{m + 1}\left(r \right)=\frac{1}{{t\left({N-n} \right)}}\sum\limits_{i=1}^{t\left({N-n} \right)} {P_i^{m + 1}\left(r \right)} $ |
(6) Pm(r)和Pm+1(r)分別表示嵌入維度為m、m+1時，兩個復合延遲向量相似性的條件概率。對于相似容限r，多元樣本熵表示嵌入維度m、m+1時兩個條件概率的比值的負自然對數
| $MSE\left({M, \lambda, r, N} \right)=-\ln \left[{\frac{{{P^{m + 1}}\left(r \right)}}{{{P^m}\left(r \right)}}} \right]$ |
1.2 改進的多元多尺度熵
改進的多元多尺度熵與傳統多元多尺度熵計算步驟相似，首先對時間序列{xk, i}i=1N, k=1, 2, …, t進行粗粒化，對于尺度ω，粗粒化后的多元時間序列
| $y_{k, j}^\omega=\frac{1}{\omega }\sum\limits_{i=\left({j-1} \right)\omega + 1}^{j\omega } {{x_{k, i}}, } $ |
其次，計算改進多元樣本熵。本文主要是對多元樣本熵的計算過程進行了改進。
改進多元樣本熵(improved multivariate sample entropy，IMSE)的計算步驟：
(1) 定義復合延遲向量Xm(i)∈Rm, i=1, 2, …, N-n，其中n=max {M}×max{λ}
(2) 定義Xm(i)與Xm(j)的距離d[Xm(i), Xm(j)]為兩者對應元素中差值最大的一個:
| $\begin{array}{c} d\left[{{X_m}\left(i \right), {X_m}\left(j \right)} \right]={\max _{n=1, 2, \cdots, m}}\left\{ {\left| {x\left({i + l-1} \right)} \right.-} \right.\ \left. {\left. {x\left({j + l-1} \right)} \right|} \right\} \end{array}$ |
(3) 對于給定的閾值r(r＞0)，對每個i值統計d[Xm(i), Xm(j)]≤r, j≠i的數目與總個數N-n-1的比值，記為，再求所有i的平均值
| ${P^m}\left(r \right)=\frac{1}{{N-n}}\sum\limits_{i=1}^{N-n} {P_i^m\left(r \right)} $ |
(4) 擴展多元延遲向量的維數從m維至m+1維。嵌入維度為m+1時，嵌入向量擴展為：
| ${M_{m + 1}}\left(i \right)=\left[{{{\left({m + 1} \right)}_1}, {{\left({m + 1} \right)}_2}, \cdots, {{\left({m + 1} \right)}_t}} \right]$ |
因此，在空間Rm+1中就可以得到N-n個復合延遲向量Xm+1(i)，Xm+1(i)表示嵌入維度從mk增加到mk+1時的復合延遲向量。
(5) 嵌入維度m+1，重復步驟(1)~(3)，得到
| ${P^{m + 1}}\left(r \right)=\frac{1}{{N-n}}\sum\limits_{i=1}^{N-n} {P_i^{m + 1}\left(r \right), } $ |
式中Pim+1(r)表示在時間尺度λ上，以X(i)為中心，在嵌入維度m+1情形下，向量mm(i)與Xm(i)的距離d[Xm(i), Xm(j)]小于等于r的概率，表示所有Xm(i)與Xm(j)的關聯程度，也就是表示序列{xk, i}i=1N的規律性程度。而均值Pm+1(r)則表示在尺度λ下的時間序列的自相關程度。
(6) 計算IMSE
| $IMSE\left({M, \lambda, r, N} \right)=-\ln \left[{\frac{{{P^{m + 1}}\left(r \right)}}{{{P^m}\left(r \right)}}} \right]$ |
傳統多元多尺度熵計算MSE時，嵌入維度為m+1，則嵌入向量中只有一組向量嵌入為m+1，其他保持不變，即Mm(i)=[m1, m2, …, mk+1, …, mt](k=1, 2, …, t)，對于每個變量嵌入N-n次，得到N-n個復合延遲向量Xm(i)。t個變量的時間序列嵌入后復合延遲向量數為t(N-n)。即多元嵌入復合延遲向量為各變量依次嵌入的累積，則距離d[Xm(i), Xm(j)]的計算出現冗余重復。
而本文提出的改進方法在嵌入維度為m+1時，嵌入向量中所有向量均嵌入為m+1，也就是Mm+1(i)=[(m+1)1, (m+1)2, …, (m+1)t]，相對于傳統方法，本文方法不再針對每一個變量，而是針對所有變量，對于t個變量，總的復合延遲向量Xm(i)數為N-n，計算任意兩個向量間的距離，比傳統t(N-n)個復合延遲向量兩兩計算距離減小了計算量，因而計算速度更快。由于實際生理信號大多通道數較多，傳統方法在信號采樣點數為1 000、通道大于10時計算量大，復雜度高，使計算機內存溢出，無法有效計算；而本文提出方法則更具有普遍適用性，即使通道數較多(如64)也能有效地計算，因而本文提出方法更能滿足實際多元時間序列的需要。
2 實驗分析
2.1 仿真分析
文獻[13]中分析了單通道時多尺度熵的特點，對于不相關的隨機白噪聲信號，其樣本熵隨著尺度的增加單調遞減；而對于具有遠程相關性的1/f噪聲信號，信號的樣本熵隨尺度的變化無明顯改變。這就說明了對于單通道信號1/f噪聲比不相關的隨機白噪聲更加復雜。為了闡明改進的多元多尺度熵具有同樣的特性，實驗分析了不相關的隨機白噪聲和1/f噪聲生成的4個3通道的時間序列信號。對于每個時間序列在計算改進的多元多尺度熵時所用參數都相同，M=2、tau=1、r=0.3×std(std表示歸一化時間序列的標準偏差)，圖 1為對應的3通道信號多元多尺度熵的變化曲線。如圖所示，隨著1/f噪聲的增加，MSE在較高尺度上逐漸增大。當3個通道都是1/f噪聲時，復雜度在高尺度上達到最大。因而采用多元多尺度熵驗證區分隨機白噪聲和1/f噪聲是十分有效且方便的。同時也可得出以下結論：在具有遠程相關的多元時間序列中，遠程相關的變量越多，系統的復雜度越高。
圖1
三通道(白噪聲、1/f噪聲)改進的多元多尺度熵分析
Figure1.
Improved multivariate multiscale entropy analysis of three channels (white noise and 1/f noise)
一般的多尺度熵只反映了單通道信號的遠程相關性，對于多通道數據，數據間的相關性及交互信息就無法有效地描述。而本文提出的改進多元多尺度熵對多元數據通道內及通道間的相關性都能進行有效的描述。
為了充分體現改進的多元多尺度熵的優越性，分別生成3通道相關1/f噪聲與不相關1/f噪聲，相關隨機白噪聲與不相關隨機白噪聲信號。文獻[14]表明傳統的多尺度方法只反映了通道內的相關性，對于多通道間相關與不相關的白噪聲與1/f噪聲不能進行有效區分。如圖 2所示，本文提出的改進的多元多尺度熵既反映了通道內的遠程相關性，又反映了通道間的相關性。對于相關與不相關的無論是白噪聲還是1/f噪聲，在某些尺度都具有良好的區分度。不相關的1/f噪聲在較高的尺度上復雜度最高，而相關白噪聲最低。由相關數據的物理意義可知，數據間的相關度越高則復雜度越小，其相應熵值也就越小；數據間的相關度越低則復雜度越大，其相應熵值也就越大。采用本文方法，不相關的1/f噪聲和白噪聲在各尺度熵值均大于相關的1/f噪聲和白噪聲，具有明確的物理意義。
圖2
改進的多元多尺度熵相關性分析比較
Figure2.
Correlation analysis comparison of improved multivariate multiscale entropy
2.2 癲癇數據實驗分析
本文數據來源于德國波恩癲癇研究室的癲癇數據庫，數據庫中含有5個數據集，依次用Z、O、N、F、S的5個字母表示，每個集合包含100個單通道EEG數據段，長度均為23.6 s。數據集Z記錄了志愿者清醒睜眼狀態的EEG，O記錄了清醒閉眼狀態的EEG，N記錄了致癇灶對側域，F記錄了致癇灶內域，都是在沒有癲癇發作時的EEG記錄，只有S記錄了致癇灶內域癲癇活動。本文針對5個數據集進行研究，其中數據集中的前50段為訓練樣本，后50段為測試樣本。
為了能有效地識別癲癇EEG信號特點，首先對癲癇EEG信號進行小波包分解。在分解的過程中，節點的選取既要覆蓋癲癇腦電波的特征頻帶，又要最大限度地節約時間和空間。因此對原始信號選取DB4小波基，進行3層小波分解。
為了將改進的多元多尺度熵與傳統的多元多尺度熵進行更好的比較，首先選取數據集Z、S進行分析。對兩種方法選取同樣的參數：M=2、tau=1、r=0.3×std (std歸一化癲癇EEG信號的標準偏差)。如圖 3所示，對原始癲癇數據進行3層小波包分解，選取同樣的頻帶范圍，對于單個頻帶計算其多尺度樣本熵，在3個頻帶范圍內兩個數據集的多尺度樣本熵均值方差曲線距離近，且在大多尺度上有明顯的交叉重疊，因而在各頻帶多尺度樣本熵不能有效地區分數據集Z、S。
圖3
單頻帶多尺度樣本熵
(a)0~10.85 Hz多尺度樣本熵；(b)10.85~21.7 Hz多尺度樣本熵；(c)21.7~32.55 Hz多尺度樣本熵
Figure3. Single band multiscale entropy of samples(a) 0-10.85 Hz multiscale samples entropy; (b) 10.85-21.7 Hz multiscale samples entropy; (c) 21.7-32.55 Hz multiscale samples entropy
對于多元信號，傳統的樣本熵無法對其進行描述，然而改進的多元多尺度熵可體現出明顯的優越性。圖 4(a)為數據集Z、S的100個樣本改進的多元多尺度熵均值方差曲線；圖 4(b)為傳統的多元多尺度熵的均值方差曲線。改進的多元多尺度熵兩個數據集的均值在各尺度上相距較遠，方差曲線在大
圖4
三個頻帶時傳統的多元多尺度熵與改進的多元多尺度熵結果比較
(a)數據集Z、S三頻帶改進的多元多尺度熵；(b)數據集Z、S三頻帶傳統的多元多尺度熵
Figure4. Comparison of three frequent bands results between traditional multivariate multiscale entropy and improved multivariate multiscale entropy(a) improved multivariate multiscale entropy of three frequent bands (dataset Z, S); (b) traditional multivariate multiscale entropy of three frequent bands (dataset Z, S)
多數尺度上無交叉重疊，因而具有良好的可分性；而傳統的多元多尺度熵均值曲線距離近，方差曲線在大多數尺度上重疊明顯，可分性差。雖然改進的方法對于一元信號沒有表現出明顯的優越性，但是對于多元信號而言，改進的方法明顯優于傳統方法。
應用本文提出的改進的多元多尺度熵，僅選取尺度1和尺度6作為特征，如圖 5所示兩類的可區分性極其顯著，即使應用簡單的分類器也能獲得很高的分類精度。因而說明應用本文提出的特征提取方法，需要很少的特征就能獲得很高的分類精度。在改進的多元多尺度熵中，各尺度上的值表示在該尺度粗粒化時間序列的多元樣本熵，如圖的兩個特征分別表示尺度1、6上的改進多元樣本熵，描述了在相應尺度上的復雜度，也就是說改進多元多尺度熵的不同尺度特征均有其物理意義。
圖5
數據集Z、S兩個尺度上改進的MSE
Figure5.
Improved MSE (Data sets Z, S) with two scales
本文提出的方法不僅在分類精度上有明顯提高，還大大提高了計算速度。為了將本文提出方法與傳統方法比較，對原始癲癇EEG信號利用小波包進行4層分解，獲取不同頻帶的數據信號，隨著通道數的增加，計算時間如表 1所示。從表 1可以看出，隨著數據長度的增加，兩種方法的計算時間都明顯增加，但是無論數據長度是多少，就多元信號而言，改進方法的計算時間都要比傳統方法短。
表1
傳統的多元多尺度熵與改進的多元多尺度熵運行時間比較
Table1.
Comparison of execution time between traditional multivariate multiscale entropy and improved multivariate multiscale entropy
最后，對不同數據集組合進行分類比較，對各數據集均選取區分度較好的尺度作為特征進行分類。本文中采用的分類器分別為概率神經網絡(probabilistic neural network, PNN)、支持向量機(support vector machine，SVM)、線性判別分類器(linear discrimination analysis，LDA)，送入到不同分類器的特征數據均相同，不同的數據集組合分類精度如表 2所示。
表2
不同分類器分類結果比較
Table2.
Comparison of classified results between different classifiers
由三種不同分類器在相同條件下的分類結果可以看出，對于本文提取出的特征, 應用相對簡單的分類器反而可以得到較高的分類精度，對各數據集最高正確率分別為100%、96.7%、90.3%。與目前國際上針對各數據集組合的特征提取與分類結果相比，本文所提出的方法體現出明顯的優越性，具體結果如表 3所示。
表3
不同特征提取及分類方法識別結果對比
Table3.
Recognition result comparison between different feature extractions and classifications
3 結論
本文提出的改進的多元多尺度熵，相對于單尺度熵能更好地反映通道內及通道間的相關性，還能夠提供更加豐富的多元觀測信號的動態特性，獲取比標準的多尺度熵更高的自由度。相對于傳統的多元多尺度熵，本文在嵌入維數為m+1時，對算法進行了改進。傳統方法對于變量k，嵌入向量擴展為Mm(i)=[m1, m2, …, mk+1…, mt](k=1, 2, …, t)，而改進方法對所有變量嵌入向量擴展為Mm(i)=[(m+1)1, (m+1)2, …, (m+1)t]。因此，在距離計算過程中，復合延時向量數為原來的1/t，解決了傳統的多元多尺度熵隨著通道數增加內存很快溢出的問題，因而更適用于實際工作中多通道的生理信號分析。
由于實際EEG信號高頻部分多為噪聲干擾，本文將小波包分解與改進的多元多尺度熵相結合，能很好地濾除干擾信號。以不同尺度上的改進的多元樣本熵作為特征，縮短了計算時間，獲得更好的癲癇EEG信號區分度。本文只將該方法用于癲癇EEG信號分析，如何應用于其他領域是下一步需要進行的工作。
